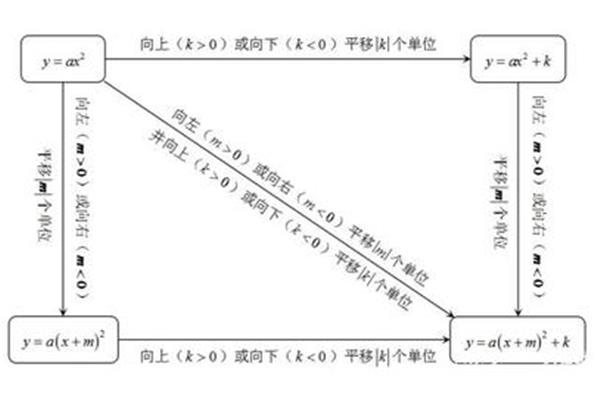
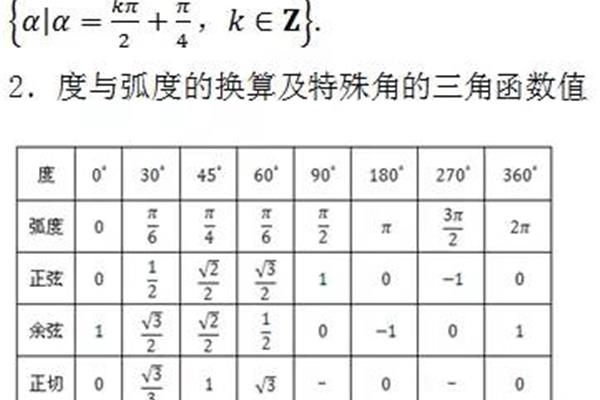
函数化为指数运算法则如下 e的幂函数运算法则
指数函数是一种特殊的函数,其自变量为指数形式,函数表达式为f(x)=a^x,其中a为底数,x为指数。指数函数运算法则如下:1,指数函数的乘法法则:a^m,幂函数是指形如$y=x^a$的函数,其中$a$是常数,以下是幂函数定义域的一些运算法则:1。如果$a$是正整数,则幂函数的定义域为正实数集$\mathbb{R}^{ }$。

具体来说,幂的方程法则包括以下几个方面:1。幂的乘法法则:a^m*a^n=a^(m n),即相同底数的幂相乘。指数函数的一般形式为y=a^x(a0且不=1),函数图形上凹,a大于1,则指数函数单调递增;a小于1大于0,则为单调递减的函数。指数函数既不是奇函数也不是偶函数。转换公式是:log(a)y=x指数函数是重要的基本初等函数之一,一般地,y=ax函数(a为常数且以a0,a≠1)叫做指数函数,函数的定义域是R。
指数函数的相加法则是:在相同的底数下,指数相同的指数函数可以相加,即$a^x a^x=2a^x$。具体地说,如果有两个指数函数$f(x)=a^x$和$g(x)=a^x$。关于幂的运算有:一,同底数幂相乘,底数不变,指数相加公式a的m次方乘以a的n次方等于a的(m n)次方(其中,m,n为正整数)二,同底数幂相除,底数不变。

(2)任何不等于零的数的-p(p是正整数)次幂,等于这个数的p次幂的倒数。即(a≠0,p是正整数)。同底数幂相乘,底数不变指数相加,即,a^n•a^m=a^(n一m)。2,同底数幂相除,底数不变指数相减,即为a^n÷a^m=a^(n一m)。同类幂加减,只把系数1。指数a的m次方乘以a的n次方等于a的m加n次方log以a为底的m的对数乘以log以a为底的n的对数等于log以a为底的(m n)的对数幂函数和指数运算差不多!。
2、幂的乘方(a^m)^n=a^(mn),与积的乘方(ab)^n=a^nb^n。3、同底数幂的除法,1、同底数幂的乘法:2、幂的乘方(a^m)^n=a^(mn),与积的乘方(ab)^n=a^nb^n。3、同底数幂的除法:(1)同底数幂的除法:am÷an=a(m-n)(a≠0,m,幂函数的定义域和值域:当m,n都为奇数,k为偶数时,定义域、值域均为R;当m,n都为奇数,k为奇数时,定义域、值域均为{x∈R|x≠0}。
![{$DT[sitename]}](/skin/zx123/img/logo.png)