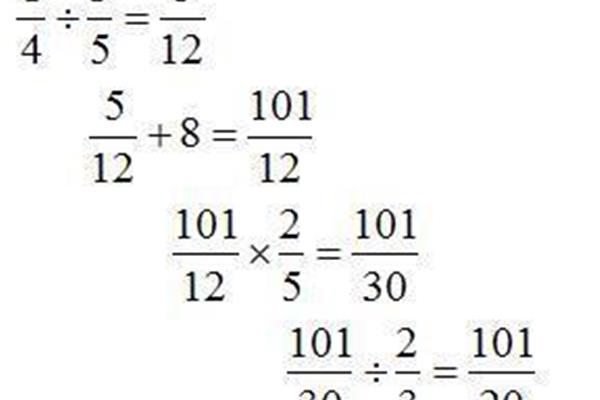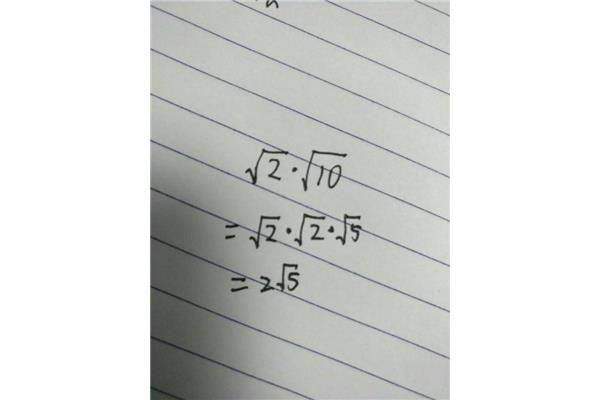根号下求导是微积分中一个重要的概念，它涉及到如何求出函数的导数。它可以帮助我们分析函数的性质，从而更好地理解函数的行为，根号下求导的概念是一个比较复杂的概念，这里将详细介绍它的概念及其应用。

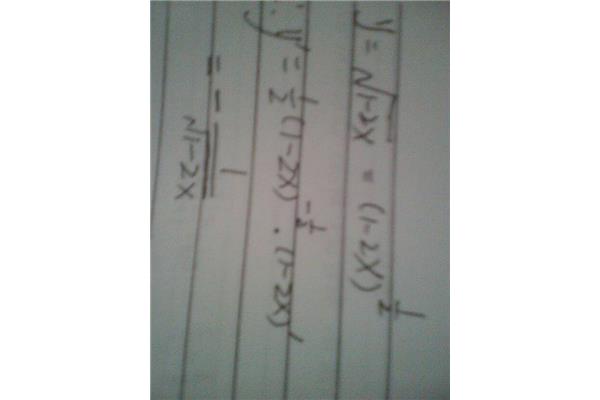
根号下求导是指求出一个函数的导数，其中函数的变量是根号下的变量。根号下求导的基本原理是，对于一个函数f(x)，它的导数是指改变x的值时f(x)的变化率。根号下求导就是求出函数f(x)在根号下变量x的变化率，也就是求出函数f(x)关于根号下变量x的导数。

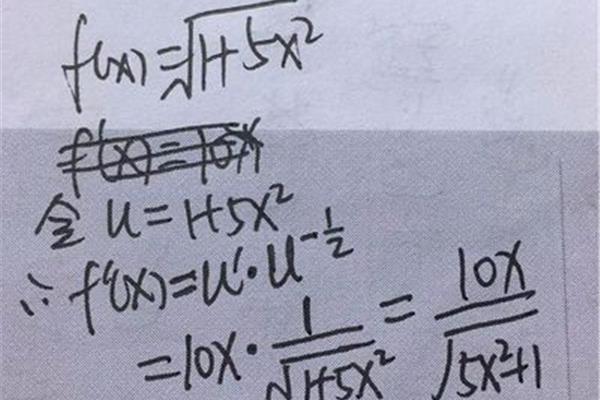
根号下求导的基本原理可以用极限的方法来推导，即当根号下变量x的变化量趋于0时，函数f(x)的变化量趋于某个值，这个值就是函数f(x)关于根号下变量x的导数。

根号下求导的应用非常广泛，它可以帮助我们求出函数的极值点、拐点等，从而更好地理解函数的行为。此外，它还可以帮助我们分析函数的性质，比如函数的单调性、凹凸性等。

总之，根号下求导是一个重要的概念，它可以帮助我们更好地理解函数的行为，从而使我们更好地分析函数的性质。此外，它还可以帮助我们求出函数的极值点、拐点等，因此，根号下求导是微积分中一个重要的概念，它的应用非常广泛。