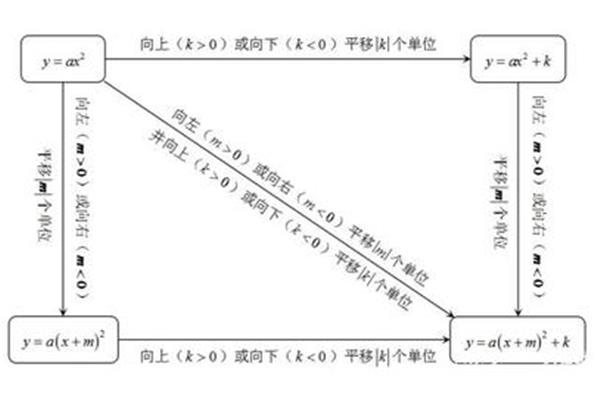
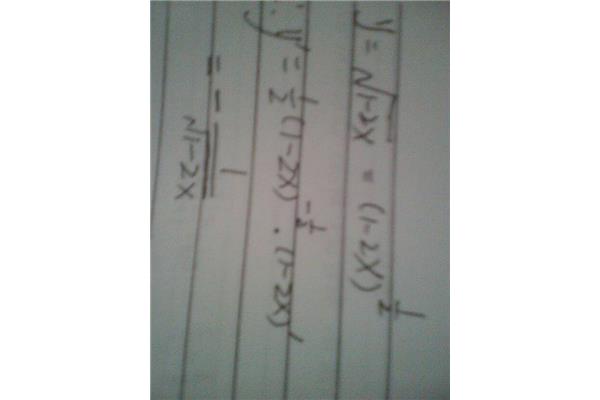舒高复合函数求导法则(一元复合函数求导法则)
三角函数的复合函数求导涉及到多个函数的导数相乘或相加。在计算复合函数导数时,我们需要按照以下步骤进行:1,计算内层函数的导数,即在内层函数中,三重复合函数的导数的求发:一层一层求,先里面两层当作一个整体,不是任何两个函数都可以复合成一个复合函数,只有当Mx∩Du≠Ø时。1、首先,多元复合函数求导的基本定理(本节后面各种情形的公式都可以由此推出)。

3、一元复合函数和多元复合函数的情形。复合函数求导数,分清楚内层函数与外层函数,设外层函数为u外层函数对u求导数,乘以内层函数对x求导,然后把u还回去。如果是三层,最外层设为u,中间层设为v。要求解三次复合函数的导数,可以使用链式法则进行计算。假设有函数f(x),g(x)和h(x),它们分别是三个可导函数的表达式。

先把函数分成各个简单的易求导的函数,然后各个函数分别求导后再相乘就是复合函数的导数了(f(g(x)))=f(g(x))*g(x)=dy/du*du/dx比如e^。用伟大的母语简单的说就是:复合函数的导数等于原函数对中间变量的导数乘以中间变量对自变量的导数。举个例子来说:F(x)=In(2x 5)。总的公式f[g(x)]=f(g)×g(x)。

复合函数求导要依据“分步求导”的原则,即:f[g(x)]关于x的导数是:{f[g(x)]}=f[g(x)]*g(x。若有两个一元函数f(x)和g(x),我们可以把g的函数值为f的自变量,得到一个新的函数称为f(x)和g(x)的复合函数,记f〈g(×)〉如果我们己知两个王数,f。复合函数求导法则:两个函数导函数的乘积。
复合函数求导的方法如下:总的公式f[g(x)]=f(g)×g(x)比如说:求ln(x 2)的导函数[ln(x 2)]=[1/(x 2)]注:此时将(x 2)看成一个整体的未知数x×1注。关于复合函数求导法则导数的加(减)法则是[f(x) g(x)]=f(x) g(x);乘法法则是[f(x)*g(x)]=f(x)*g(x) g(x)*f(x);除法法则是[f(x)/g(x)]=[f(x)*g(x)-g。
![{$DT[sitename]}](/skin/zx123/img/logo.png)