正切二倍角公式是一种计算三角函数的公式，它可以用来计算一个角度的正切值的两倍。正切二倍角公式是三角函数的基本公式之一，它可以用来计算任意角度的正切值的两倍。

正切二倍角公式的表达式如下：

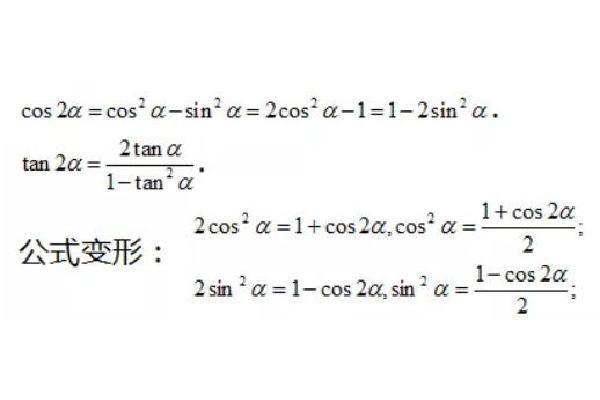
tan2θ=2tanθ/(1-tan2θ)

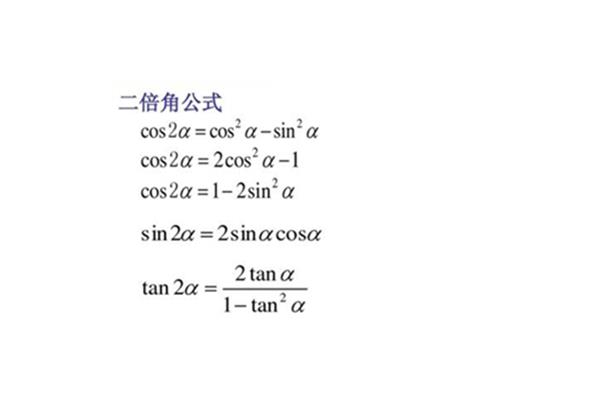
其中，θ表示角度，tanθ表示正切值。

正切二倍角公式可以用来计算任意角度的正切值的两倍，这是因为tan2θ的值等于2tanθ/(1-tan2θ)。因此，只要知道角度θ的正切值，就可以用正切二倍角公式来计算该角度的正切值的两倍。

正切二倍角公式也可以用来计算任意角度的正切值。例如，如果已知角度θ的正切值tanθ，那么可以用正切二倍角公式来计算该角度的正切值：tanθ=2tan2θ/(1-tan2θ)。

正切二倍角公式还可以用来计算角度θ的余切值。例如，如果已知角度θ的正切值tanθ，那么可以用正切二倍角公式来计算该角度的余切值：cotθ=1-2tan2θ/(1-tan2θ)。

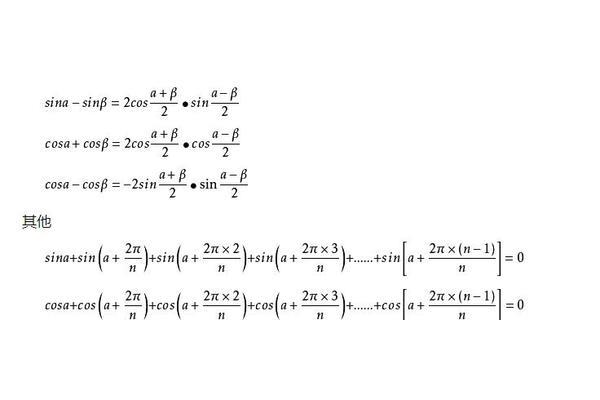
正切二倍角公式也可以用来计算角度θ的正弦值和余弦值。例如，如果已知角度θ的正切值tanθ，那么可以用正切二倍角公式来计算该角度的正弦值和余弦值：sinθ=2tanθ/(1 tan2θ)，cosθ=1/(1 tan2θ)。

正切二倍角公式是一种常用的计算三角函数的公式，它可以用来计算任意角度的正切值的两倍，以及该角度的余切值、正弦值和余弦值。正切二倍角公式的使用比较简单，因此在计算三角函数时，它是一种非常有用的工具。