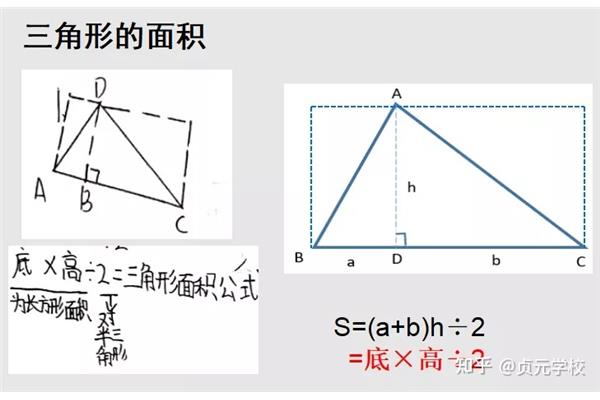
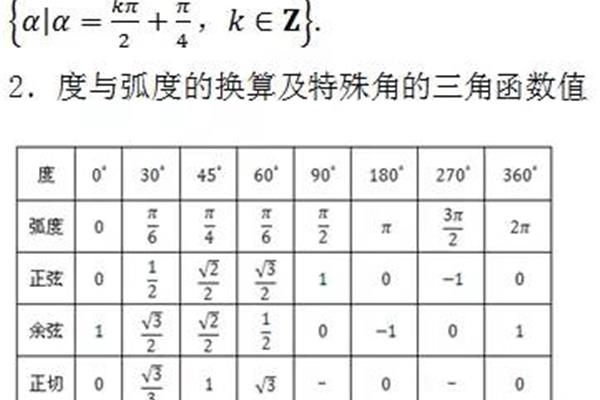
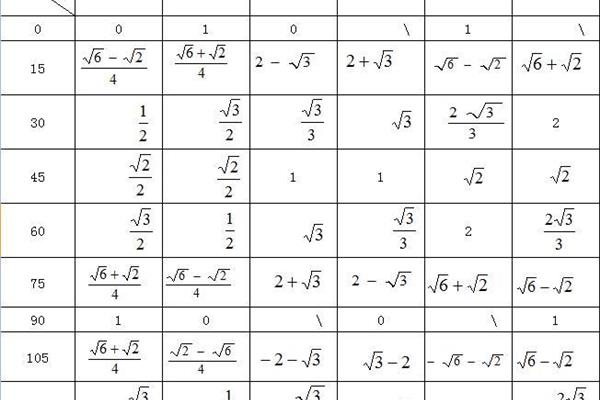
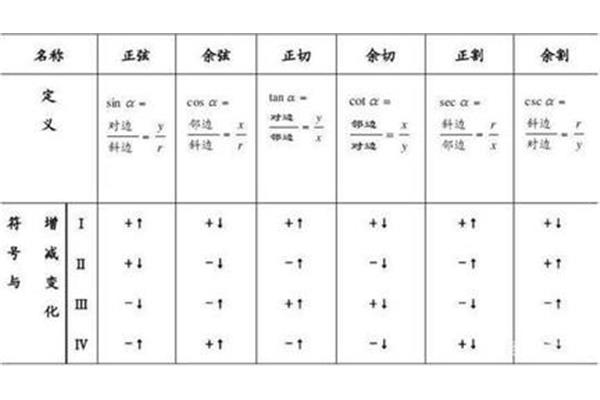
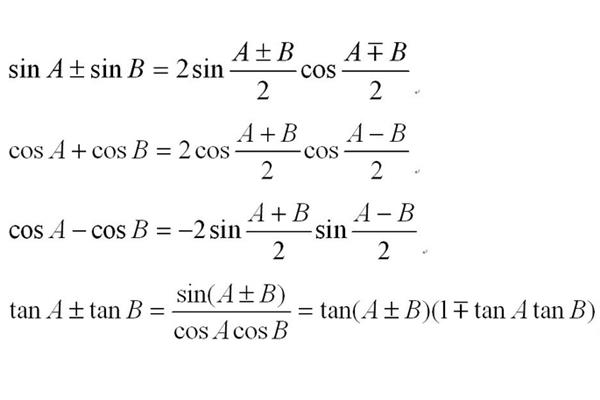三角函数诱导公式口诀:奇变偶不变符号看象限
诱导公式口诀:奇数变量不变。接下来,我们分享一下三角函数归纳法的公式,急:Math 诱导公式口诀奇偶变化不变,符号看象限,三角函数归纳法的公式(奇数变量为常数,符号取决于象限),三角函数归纳出公式1到公式5的函数名没变,公式6的函数名变了的规律。三角函数归纳法公式的规律公式归纳法的公式是指利用周期性将大角度的三角函数转化为小角度的三角函数的公式。
方法一:sin(π α)sinαcos(πα)-cosαtan(πα)sinαcos(πα)-cosαtan(πα)-tanα按sin、cos、tan的顺序记录,这两个公式是πα的前两个负号。π-α之后的两个负号sin(-α)-sinαcos(-α)cosαtan(-α)-tanαsin(2π-α)-sinαcos(2π-α)cosαtan(2π-α)-tanα是-α两边的负号(也就是第一个和第三个因为它不随2π变化也不随2π变化)sin(π/2α)cosαcos(π/2α)-sinαsin(π/2-α)cosαcos两个正弦;三条切线;四余弦”。
例如sin(x nπ/2)奇偶性指n,当n为偶数时,三角函数的名称不变,或者sin符号指X为锐角的象限然后计算(x nπ/2)。如果这个象限的正弦值为正,那么它为正,那么它为负,当n为奇数时,那么它为负。三角函数归纳法的公式(奇数变量为常数,符号取决于象限)。

比如计算:sin240tan 240 sin 240 sin(180 60)sin 60;sin240sin(27030)cos30 .上面的180度是90度的偶(2)次,结果还是原函数(正弦),而270度是90度的奇(3)次,结果变成原函数的余函数(余弦),因为240度的原角是第三项的角,原函数的符号是负的。

常用归纳公式SIN(90°α)COSαSIN(90°α)COSαCOS(90°α)SINαSIN(270°α)COSαSIN(270°α)COSαCOS(270°α)SINαSIN(180°α)SINαCOS(180°α)COSαCOS(360°α)SINαSIN(360°α)SINαCOS(360°α)COSαCOS(360°α)COSα观察上述

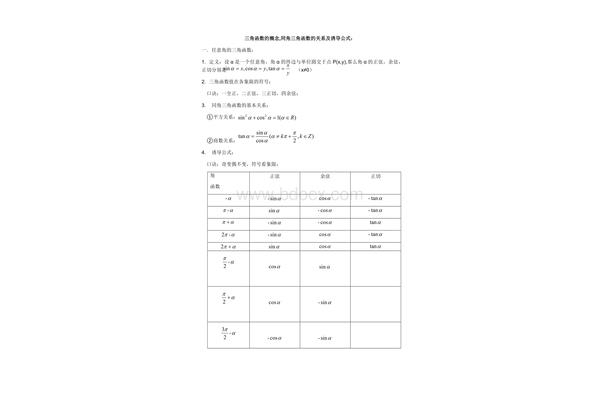
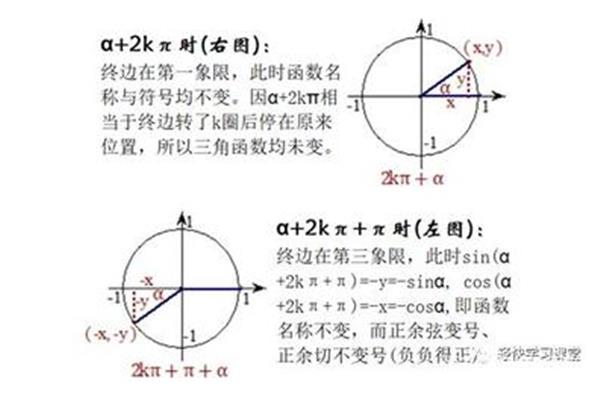
归纳公式三角函数的基本公式如下:sin(2kπα)sinα(k∈z)cos(2kπα)cosα(k∈z)tan(2kπα)tanα(k∈z)cot(2kπα)cotα(k∈)。

常用的归纳公式有以下几组:公式1:设α为任意角度,同一个角的同一个三角函数具有相同的终边的值相等:Sin(2kπ α)= Sinαcos(2kπ α)= cosαtan(2kπ α)= tanαcot(2kπ α)= cotα公式2:设α。π α的三角函数值与α的三角函数值的关系:sin(π α)=-sinαcos(π α)=-cosαtan(π α)= tanαcot(π α)= cotα公式3:任意角度α与α的三角函数值的关系:sin (-α) =-sin α cos。等式4:利用等式2和等式3可以得到π α和α三角函数值的关系:sin(π-α)= sinαcos(π-α)=-cosαtan(π-α)=-tanαcot(π-α)=-cotα等式5:利用等式1和等式3可以得到π α和α三角函数值的关系:
归纳公式是指利用周期性将一个大角度的三角函数转化为一个小角度的三角函数的公式。接下来分享三角函数归纳法的公式。三角函数归纳出公式1到公式5的函数名没变,公式6的函数名变了的规律。公式一至公式五可以缩写为:函数名不变,符号看象限。即αk 360°(k∈z)、﹣ α、180°α、360°-α的三角函数值等于α的同名三角函数值,前面加一个当α视为锐角时原函数值的符号。

奇偶变量保持不变,符号取决于象限。关于180°α、360°α和-α的诱导公式口诀:函数名不变,符号取决于象限。关于90°α,270°α诱导公式口诀is:函数名变化,符号取决于象限。说明:①无论α角是什么,都视为锐角来确定归纳公式中该角的象限,从而确定其符号。符号的确定是由原函数的角度所在的象限决定的。(3)函数名的变化是指正弦和余弦、正切和余切、割线和余切的相互变化。

三角函数诱导公式口诀如下:一是全正,二是正弦,三是正切,四是余弦;All,s,t,c,阳性;奇变偶,符号看象限;正弦一,二,一,三,余弦一,四紧密相连,而且是正的。一个正正弦、两个正正弦、三个正切、四个余弦1和第一象限内任意一个角的四个三角函数都是“”;2.第二象限只有正弦是“”,其余都是“”;3.在第三象限中,只有切线和余切是“”,其余都是“”;
all、s、t、c和正ト的公式,是指第一象限内任意角度的四个三角函数为“”;第二象限只有正弦是“”,其余都是“”;只有第三象限的切线是“”,其余都是“”;第四象限只有余弦是\\,其余都是\ \。奇、偶为常数,象限“奇、偶”的符号指元/2的倍数的奇偶性,“变、常数”指三角函数名称的变化;“变”是指正弦变余弦,正切变余切。
![{$DT[sitename]}](/skin/zx123/img/logo.png)