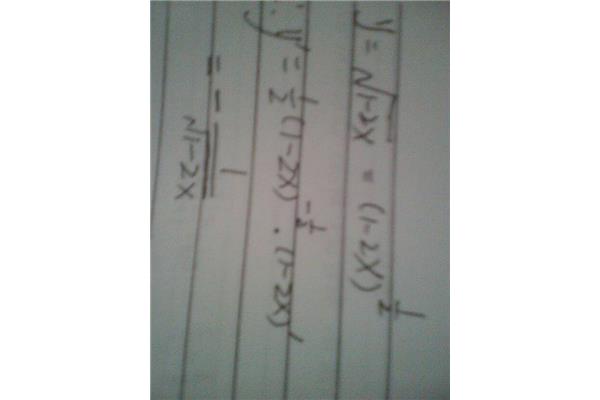定积分怎么推导？关于定积分的推导公式！{∫(0，“求定积分”和“求定积分的导数”有什么区别？如何对定积分公式求导，使积分的上下限为常数？如果f(x)的积分上下限不变，当然是0，或者我们可以提取未知量去求导，得到常数。反正这里的导数和积分无关，如何求解定积分的导数:定积分是常数，常数的导数为0，“求定积分”和“求定积分的导数”的区别和解决方法如下:1，定义不同1。求定积分本质上讲的是函数的原函数，即函数f(x)在区间上的定积分导数为0，是一个常数，而求不定积分导数的结果就是在被积函数上加一个常数，一个函数可以有不定积分，但不能有定积分；也可以有定积分，但是没有不定积分，一个连续函数必然有定积分和不定积分；如果只有有限个不连续点，则定积分存在；如果有跳跃不连续，原函数一定不存在，也就是不定积分一定不存在，定积分定理:将函数在一定区间内的图像[a，b]分成n份，用平行于Y轴的直线分割成无数个矩形，然后求n→ ∞时所有这些矩形面积之和。

1.yc(c为常数)y 02。yx ny NX (n1) 3。你是xy a xlnaye xy e x4。ylogyy logae/xylnxy 1/X5。ysinxy cosx6。Sin 2x9。yarcsinxy 1/√ 1x 210。yarccosxy 1/√ 1x 211。yarctanxy 1/1x 212。yarccotxy 1/1x 2求导过程中需要用到的常用公式有几个:1.yf“求定积分”。从右到左？这是几个复合导数公式叠加的结果。首先，d(uv)/dtuv uv ，其中uat、V和V是V对该指数的导数。使用复合导数公式DV/DTE f(t) * F (T)，其中f(t)为定积分，最后使用F的导数。

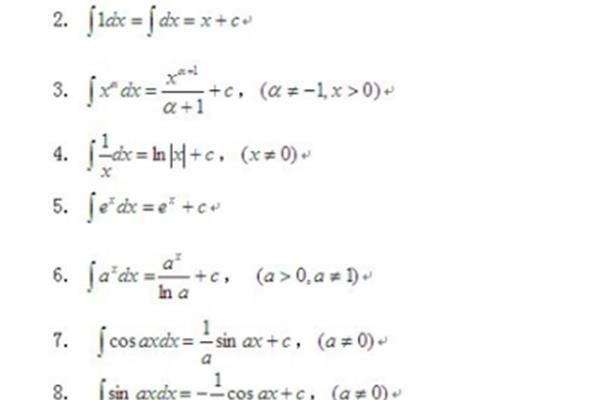
解法:定积分是常数，常数的导数为0，定积分的导数为0。例:积分是12x 2dx 1/3x 3/121/3(81)7/3(7/3) 0。对任意定积分abf(x)dxA(A为常数)，两边求导。如果f(x)的上下界是常数，当然是0，或者我们可以提取未知数得到定积分，得到常数。反正这里的导数和积分无关。它可以通过区间可加性分解为积分上限函数。比如∫(0 ~ 2)f(t)dt∫(0 ~ x)f(t)dt∫(x ~ 2)f(t)dt∫(0 ~ x)f(t)dt∫(2 ~ x)

这个求导的结果当然不是0。我们首先要理解定积分的概念。如果定积分的形式是∫(a到b)f(t)dt，(a和b是常数)，这种积分的结果是常数，它的导数当然等于0。但如果定积分的形式是∫(a到x) f (t) dt，(。但不等于0。这种积分是可变上限定积分，不同于普通定积分。d/dx∫(a到X) (XT) F (T) DTD/DX [∫ (A到X) (XT) D {∫ (0，X) [(XT) F (T))。X) TF (t) dt} ∫ (0，x) f (t) dtxf (x) xf (x) ∫ (0，x) f (t) dt(应该是变限积分求导，定积分是常数，求导的结果应该是0)。与导数相反。比如f(x)x平方的导数是f(x)2X，那么对应的就是2X，x的平方积分反过来就是微积分和数学分析中的一个核心概念。

直观地说，对于给定的正实函数，实数区间内的定积分可以理解为坐标平面上由曲线、直线和轴围成的曲线梯形的面积值(一个确定的实值)。波恩哈德·黎曼给出了积分的严格数学定义(见“黎曼积分”)，黎曼的定义使用了极限的概念，把一个弯曲的梯形想象成一系列矩形组合的极限。从19世纪开始，随着各种集成领域中各种类型函数的集成，逐渐出现了更高级的集成定义。