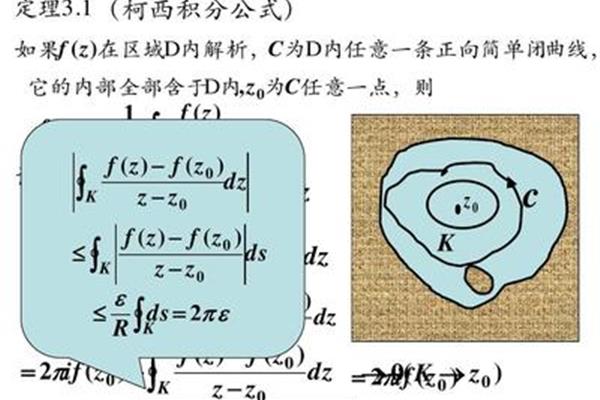
柯西积分定理说明:结果不等于零
柯西积分定理描述。柯西积分定理(或柯西-古萨定理)是关于复平面上全纯函数的路径积分的一个重要定理,第三个问题,柯西古萨定理怎么用不清楚柯西积分定理(或柯西古萨定理),这是关于复平面上全纯函数的路径积分的一个重要定理,若f是f的复倒数,则可由柯西积分定理推出柯西积分公式和留数定理,柯西积分定理的结果不等于零;这里不能使用柯西积分定。

柯西积分定理(或称柯西-古萨定理)是关于复平面上全纯函数的路径积分的一个重要定理。柯西积分定理说明了如果从一点到另一点有两条不同的路径,且函数在两条路径之间处处全纯,则函数的两条路径积分相等。另一个等价的说法是,沿任意可解闭曲线的单连通闭区域上的全纯函数的积分为0。设是复平面的单连通开子集。是域上的全纯函数。

Let f (z) 1/(z1)。∴ f(z)在z √2时有三个一阶极点ZKE (2kπ i/3),k0,1,2。从柯西积分定理,原公式(2πi)∑Res不充要。柯西基本定理:如果从一点到另一点有两条不同的路径,并且函数在两条路径之间处处全纯,那么函数的两条路径积分相等。柯西积分定理(或柯西-古萨定理)是关于复平面上全纯函数的路径积分的一个重要定理。柯西积分定理描述。如果从一点到另一点有两条不同的路径,并且函数在两条路径之间处处全纯,那么函数的两条路径积分相等。
柯西中值定理是拉格朗日中值定理的推广,是微分学的基本定理之一。它的几何意义是参数方程表示的曲线上至少有一点,其切线平行于两端所在的弦。这个定理可以看作是参数方程下拉格朗日中值定理的表达式。柯西中值定理大致说明,对于给定的两个端点之间的平面弧,至少有一个点,使得曲线在该点的切线平行于两个端点所在的弦。

1。Goursat的证明使用了李松寒的重积分的概念,使得证明更加直观明了。2.古尔萨特的证明给出了解析函数的构造方法,对实际中解决问题具有重要意义。3.Goursat的证明方法更加简洁,减少了大量的冗余计算,证明更加美观。4.柯西积分定理也适用于一些比较复杂的曲线。

在复变量里吧?扩展的柯西积分定理与柯西积分公式相同,在区域内是解析的,如果边界连续可以使用。但由于表达式不同,柯西积分定理主要利用了闭曲线上积分为0的性质,即积分与路径无关,类似于实分析中的格林公式;柯西积分公式利用闭曲线的积分来计算曲线内部的函数值,不存在0的积分(由于积分公式的结构,被积函数在闭曲线上具有奇异性);

∮cf(z)/zzodz在佐点不是解析的,所以柯西积分定理不能用,只能用柯西积分公式;柯西积分定理只能在被积函数在积分曲线C围成的区域内分析,积分为零时应用;当被积函数在积分曲线C包围的区域内不解析,且被积函数为f(z)/zzo形式时,应用柯西积分公式。
6、 柯西积分定理的结果不等于零;这里不能使用柯西积分定理该定理的一个重要结果是,单连通域中全纯函数的路径积分可以用类似微积分基本定理的方法计算:设U为C的单连通开子集,f:U→C为全纯函数,设γ为U中的分段连续可微路径,起点为A,终点为b,若f为f的复倒数,则可由柯西积分定理推出柯西积分公式和留数定理。
![{$DT[sitename]}](/skin/zx123/img/logo.png)