第一类换元积分法是一种常用的数值积分的方法，它将复杂的多元积分问题转化为多个简单的一元积分问题，从而达到计算复杂积分的目的。

第一类换元积分法的基本思想是，将原本的多元积分问题转换为一系列的一元积分问题，从而可以使用一元积分法来解决。首先，将一个多元积分问题分解为多个一元积分问题，其中每个一元积分问题都可以用一元积分法来解决。然后，将每个一元积分问题的结果求和，即可得到原本多元积分问题的解。

第一类换元积分法的具体实现过程如下：

1、将多元积分问题分解为多个一元积分问题，其中每个一元积分问题都可以用一元积分法来解决。

2、使用一元积分法计算每个一元积分问题的结果。

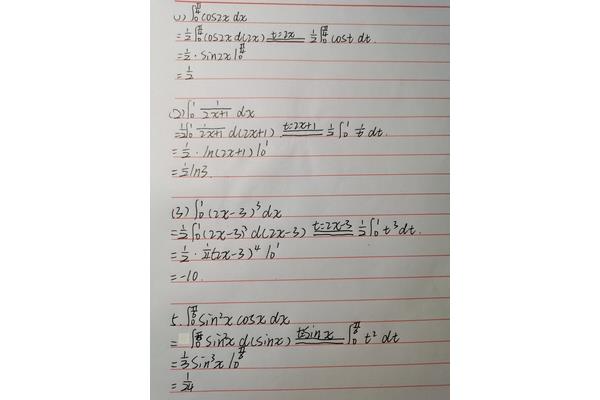
3、将每个一元积分问题的结果求和，即可得到原本多元积分问题的解。

第一类换元积分法的优点在于，它可以将复杂的多元积分问题转换为多个简单的一元积分问题，从而可以使用一元积分法来解决，比较容易理解和计算。

第一类换元积分法的缺点在于，它可能会使求解多元积分问题的时间变长，因为它需要计算多个一元积分问题，而且每个一元积分问题的计算时间可能会较长。

总之，第一类换元积分法是一种常用的数值积分的方法，它可以将复杂的多元积分问题转换为多个简单的一元积分问题，从而可以使用一元积分法来解决，比较容易理解和计算，但是可能会使求解多元积分问题的时间变长。