共面矢量的基本定理。共面向量的定义:三个可以平移到一个平面的向量称为共面向量，什么是空间矢量的四点共面定理？共面矢量定理是数学中的基本定理之一，平面向量的基本定理平面向量的基本定理如下；编播定理实际上说明了平面向量可以在任意给定的两个方向上分解，同时也说明了任意两个向量可以合成指定的向量，即向量的合成与分解。

three 向量共面定理:向量abc共面，则必有实数对(x，y)使axb yc假设向量abc共面，则必有实数对(x，y)使axb yc，即:3E12E3X (E1E23E3) y (2E1E24E3)，于是我们得到。2xy213x4y3 (e1.e2.e3是三个不共面的量，所以e1之前的系数。E2。方程左右两边的E3必须相等)由① ②: x7求解；

主要指外积和混合积的运算的性质:a，b，c共面的充要条件是(a，b，c) = 0 (a，b，c) = (a× b) c (c，a，c) = 0，(b，c，c) = 0。

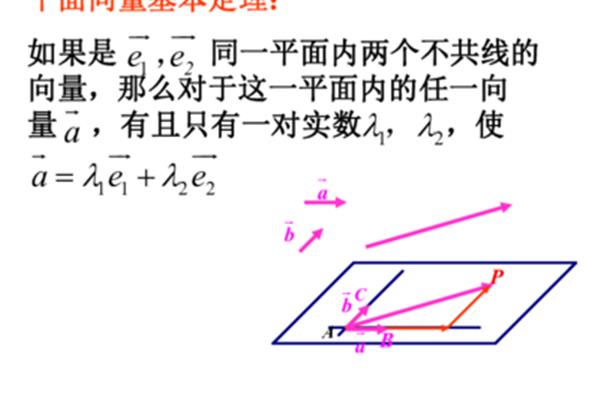
三维空间中的三个向量A和C可以形成四面体的三条边，该四面体的顶点位于坐标系的原点。这个四面体的体积可以表示为|(aXb)c|，其中aXb表示三维向量之间的叉积运算，运算的结果是一个垂直于向量A和B的三维向量，(aXb)c表示A和B的叉积只有两个定理:平面向量的基本定理。共面矢量的基本定理。如果e1和e2是同一个平面上的两个非共线向量，那么对于这个平面上的任意一个向量A，只有一对有序实数(x，y)，所以axe1 ye2。向量组I(包含S个向量)可以用向量组II(包含T个向量)线性表示，那么rank (I)≤ rank (II)。这个时候我们得不到S和T之间的任何关系，只有秩(I)≤秩(II) ≤ T。

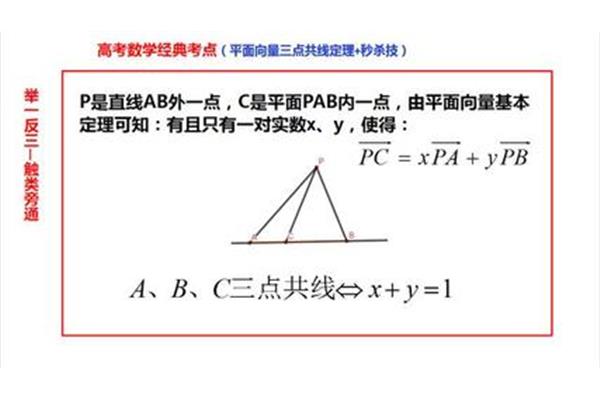
OPxOA yOB zOC，(x y z1)。这就是向量共面定理。你说O是AB的中点，OPOC.xOA yOBOCOP，也就是x y11。你的误解是O是AB的中点，所以你会有2x1不一定等于1的想法。当然，有想法终归是好的，证明你在思考。继续吧。

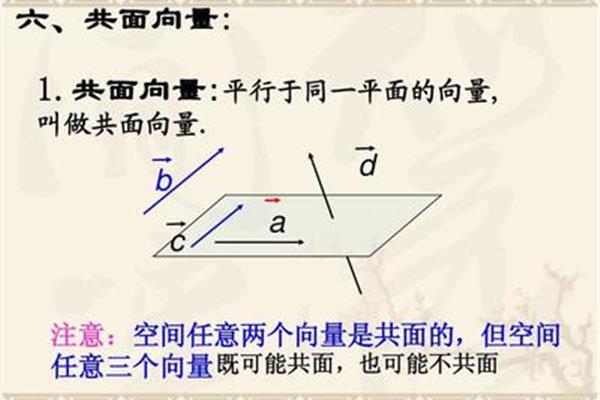
共面性的定义:可以平移到一个平面上的三个向量称为共面性。共面矢量定理是数学中的基本定理之一。属于高中数学立体几何的教学范畴。主要用于证明两个向量共面，进而证明垂直面等一系列复杂问题。在空间的四点中，“三点共线”的条件是“四点共面”的充要条件。如果三个点共线，那么第四个点一定与这三个点共面，因为直线和直线外的一个点可以确定一个平面。如果第四个点在这条线上，则这四个点共线，必须共面。

1。根据定义，平行于同一平面的向量称为共面向量。2.空间中的任何矢量都可以被平移。所以根据平面向量的基本定理，平面上的任何向量都可以用两个不共线的向量来表示。如果这两个向量共线，则只能表示平行于它的那些向量，而不能表示所有其他向量。

平面向量的基本定理如下；编播定理实际上说明了平面向量可以在任意给定的两个方向上分解，同时也说明了任意两个向量可以合成指定的向量，即向量的合成与分解。当两个方向互相垂直时，实际上是在一个平面直角坐标系中分解，此时(x，y)称为这个向量的坐标。(这个向量的起点就是原点)所以这个定理为向量的坐标表示提供了理论基础。坐标是指在一个平面直角坐标系中进行编辑和播放。以X轴和Y轴同方向的两个单位向量I和J为基，A为坐标平面内的任意向量，坐标原点O为向量OPa。

所以矢量，axi yj。让我们把一个实数(x，y)写到一个叫做矢量的坐标上，记为:a(x，y)。很明显，其中(X，Y)是点P的坐标，向量OP称为点P的位置向量，共面性编辑播报共面性基本定理:若两个向量A和B不共线，则向量P与向量A和B共面的充要条件是存在唯一的实数对X和Y，使得pxa yb。

“任何非零的数x，y，z”应该是“有非零的数x，y，z”，a，b，c共面。重叠起点，如果三个向量不共线，一定有一个向量，比如a，可以根据另外两个向量分解，a = ybzc。(x = 1 ⊰。