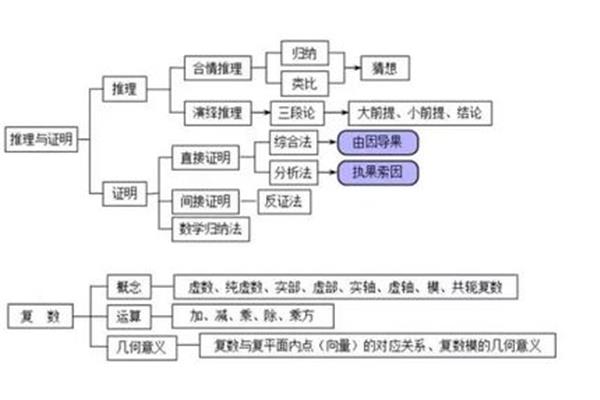
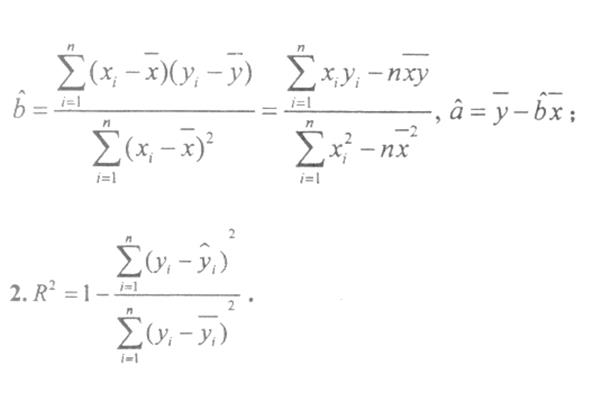余弦定理推导过程,这是平面几何方法
高中数学学习,带浙江高三学员复习完向量的知识,包括很多的拓展知识和题型,选修三的样本相关系数,教材上都有利用向量法推导,正余弦定理用向量法推导,两角差的余弦定理用向量法推导,柯西不等式用向量法推导,点到直线的距离用向量法推导,向量的威力很大,无孔不入,单看教材没太多内容,也很简单,拓展内容就很丰富。接下来开启解三角形的学习,高考基本上会考一道大题,内容也不多,有三角函数打底子,有基本的函数思想,学起来不会太难,学习的过程中依然要重视结论的来龙去脉的了解和推导。
1、 余弦定律的 推导?这是平面几何的方法。在任何△ABC,AD⊥BC.的对面∠C是C,B的对边是B,A的对边是A,还有BDcosB*c和AD SINB * C. DCBCBDacosB*c根据毕达哥拉斯定理,我们可以得到:AC 2ad 2 DC 2b 2(SINB * C)2 (Acosb * C)2b 2(SINB * C)2 A 2ac * COSB 。
2、 余弦 定理是怎么 推导的?在任何△ABC中,\x0d\x0a是AD⊥BC.\x0d\x0a∠C与c相对,∠B与b相对,∠A与a相对\x0d\x0a,还有BD cosb * c .x0aac^2ad^2 dc^2\x0d\x0ab^2(sinb*c)^2 (acosb*c)^2\x0d\x0ab^2sin^2b*c^2 a^2 cos^2b*c^22ac*cosb\x0d\x0ab^2(sin^2b cos^2b)*c^22ac*cosb a^2\x0d\x0ab^2c^2 a^22ac*cosb\x0d\x0acosb(c^2 a^2b^2)/2ac。
3、 余弦 定理的 推导?在任何△ABC,AD⊥BC.的对面∠C是C∠B的对边是B∠A的对边是A还有BDcosB*c和AD SINB * C. DCBCBDacosB*c可以根据毕达哥拉斯定理:AC 2ad 2 DC 2b 2(SINB * C)2 (Acosb * C)2b 2 sin 2b * C 2 A 2 COS 2b *得到。
![{$DT[sitename]}](/skin/zx123/img/logo.png)