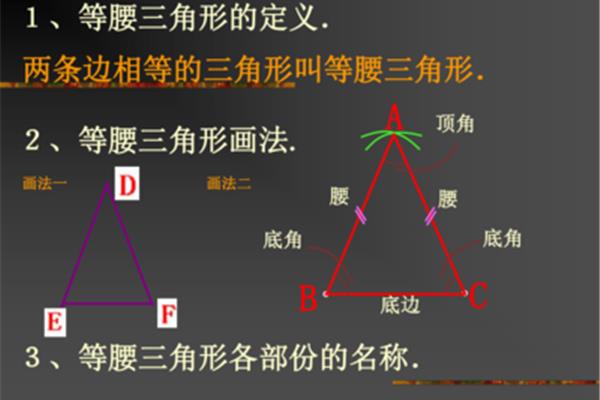
三角形的内角和定理是什么啊?
三角形内角和定理证明,什么是三角形内角和定理?球面三角形内角之和与公式三角形内角和定理表示三角形内角之和等于180。三角形内角和定理:三角形的三个内角之和等于180,什么是多边形内角和定理?三角形的内角之和等于三个内角之和,三角形内角和定理,又称三角形内角之和,是指任意三角形的三个内角之和等于180度(或π弧度)。

内角之和:180(n2),其中n指多边形的边数;你是对的。所有多边形(包括凸多边形和凹多边形)的外角之和为360度。你好!是(n2)*180度。(N是多边形的边数!)多边形的外角之和是360度。这句话没错,也是结论!希望我的回答能帮到你,让你满意。谢谢你。是多边形的外角和360度的多边形的内角之和的公式:180(n2)。

(N2) * 180 n是多边形的边数。正多边形内角之和内角和定理n等于(n-2) × 180 (n大于等于3,n为整数)。(1)任意凸多边形的外角之和等于360°;(2)多边形对角线的计算公式:N边形的对角线数等于1/2n(n3);(3)在一个平面内边和内角相等的多边形称为正多边形。【必须同时满足两个条件】反例:矩形(所有内角相等,但所有边不一定相等);菱形(等边,不一定等内角)。

多边形内角之和的公式为(N2) × 180,其中n为多边形的边数。Polygon 内角和定理 Proof:取N边形中的任意一点O,将O与每个顶点相连,将N边形分成N个三角形。因为这N个三角形的内角之和等于n 180,所以以O为公共顶点的N个角之和是360。所以N边形的内角之和是N ^ 180 ^ 2×180(N2)180。(N是边数),即N边形的内角之和等于(N2) × 180。
注:该定理适用于所有平面多边形,包括凸多边形和平面凹多边形。2.在平面多边形中,等边的凸多边形和凹多边形的内角之和相等。但是空间多边形不适用。可逆使用:N边(内角和÷ 180) 2。在N边形的一个顶点上有(n3)条对角线。n多边形的对角线为n×(n3)÷2。3.N个多边形经过一个顶点引出所有对角线后,推断多边形被分成n2个三角形:(1)任意凸多边形的外角之和等于360。
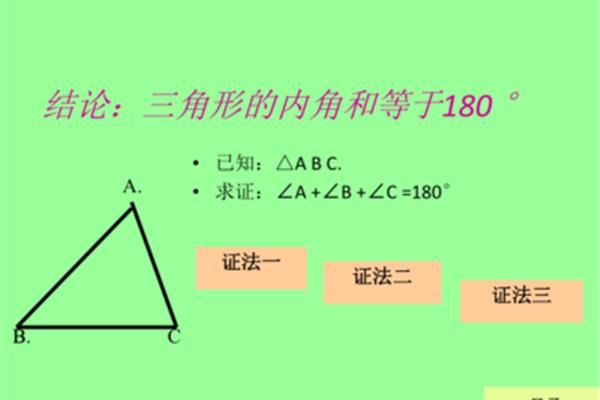
n多边形的内角和(n-2)x180度(n≥3,n为整数)。内角和公式:(n-2) × 180 (n大于等于3,n为整数),则多边形各内角的度数为:(n-2) × 180 ÷ n .多边形内角和定理的推导以及利用方程的思想计算多边形的内角和外角。在平面多边形中,等边的凸多边形和凹多边形的内角之和相等。但是空间多边形不适用。N边形的内角之和是(n2)*180度。

三角形内角和定理的两个推论如下:推论1:三角形的一个外角等于与其不相邻的两个内角之和。推论2:三角形的一个外角大于不与之相邻的任何一个内角。所以答案是:三角形的一个外角等于两个不相邻的内角之和;三角形的外角大于与其不相邻的任何内角。4、球面三角形内角和公式
triangle 内角和定理表示三角形的内角之和等于180。三角形内角和定理:三角形的三个内角之和等于180。用数学符号表示如下:在△ABC中,由∠ 1 ∠ 2 ∠ 3180推导出一个直角三角形的两个锐角。推论2三角形的一个外角等于两个不相邻的内角之和。推论3:三角形的一个外角大于任何不与之相邻的内角。三角形内角之和是外角之和的一半。三角形的内角之和等于三个内角之和。
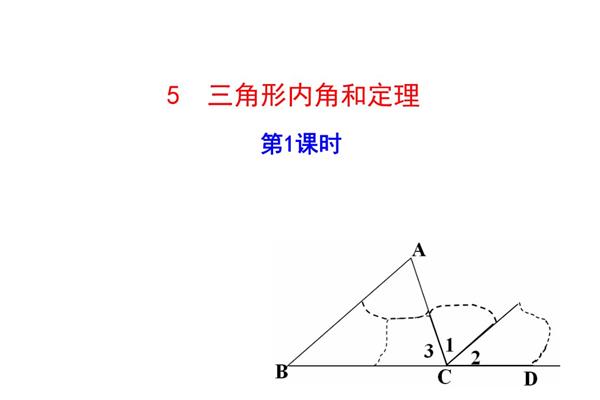
三角形的一个顶点与对边平行,顶点有三个角,加起来是180度。然后通过平行关系将三个角中的两个换成内角,得到证明2。随意画一个平行四边形,分成两个三角形,两个三角形全等。然后,平行四边形的两个邻角加起来是180度,可以求出三个角之和是180。并且其中两个角是一个三角形的内角,另一个角也可以通过平行线关系被这个三角形的内角代替,从而证明3。随意做一条三角形的高线,然后通过高线所在边的一个顶点做一条高线的平行线,然后证明高线所除的三角形的两个内角是互补的(和等于90度,很简单不解释),再对另一个三角形的两个做同样的操作。
定理:多边形内角和定理N个多边形的内角之和等于:(n-2) × 180 (n大于等于3,N为整数),边数为360÷(180-内角)。推断任意正多边形的外角与360°正多边形的任意两条相邻边形成的三角形是等腰三角形的内角及其定义【证明1:取N边形中任意一点O,将O与各顶点相连,将N边形分成N个三角形。因为这N个三角形的内角之和等于N ^ 180,所以以O为公共顶点的N个角之和为360,所以N多边形的内角之和为N . 180 ^ 2×180(N2)180。也就是说,N边形的内角之和等于(N2 )× 180。证明2:连接多边形任意顶点A1与其不相邻顶点的线段,将N边形分成(n2)个三角形。因为这(n2)个三角形的内角之和等于(n2) 180,所以N边形的内角之和是(N2) × 180。证明三:取N边多边形任意边上的任意点P,连接该点P与其他不相邻顶点的线段可以将N边多边形分成(n1)个三角形。

triangle 内角和定理,又称三角形的内角和性质,是指任意三角形的三个内角之和等于180度(或π弧度)。这个定理是三角形几何中的基本性质之一,也是众所周知的事实。具体来说,对于任意三角形ABC,其三个内角分别为∠A、∠B和∠C。三角形内角和定理说明定理∠ A ∠ B ∠ C180(或π弧度)的证明可以根据几何学的基本概念和性质进行。

然后利用直线上的角补定理可以得到∠BAD ∠ b180(或π弧度),因为∠BAD是一条直线与∠ b的补,然后以b点为中心画一条线段BE作为另一边的延伸。同样,利用直线上的角补数定理可以得到∠CBE ∠ C180(或π弧度),因为∠CBE是直线和∠ C的补数,最后我们注意到∠ bad ∠ CBE ∠ A360(或2π弧度),因为它们形成的三条线段构成一个完整的圆。
8、多边形 内角和定理Polygon 内角和定理证明方法一:取N边形中的任意一点O,将O与每个顶点相连,将N边形分成N个三角形。因为这N个三角形的内角之和等于N ^ 180,所以以O为公共顶点的N个角之和为360,所以N多边形的内角之和为N . 180 ^ 2×180(N2)180,也就是说,N边形的内角之和等于(N2 )× 180。证明2:连接多边形任意顶点A1与其他顶点的线段,将N边形分成(n2)个三角形,因为这(n2)个三角形的内角之和等于(n2) 180,所以N边形的内角之和是(N2) × 180。证明三:取N边多边形任意一边的一个点P,连接该点P与其他顶点的线段可以将N边多边形分成(n1)个三角形,这个(N2) × 180。
![{$DT[sitename]}](/skin/zx123/img/logo.png)