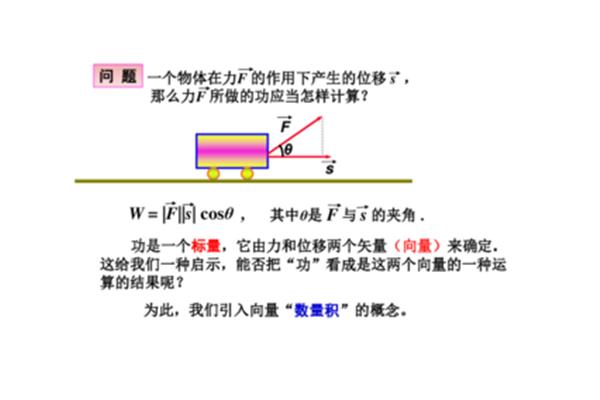
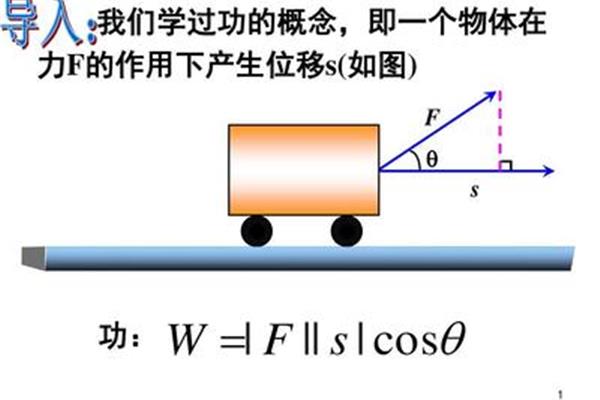
高二数学必修四教案之一:平面向量的数量积
如何理解高二必修数学四教案中平面向量的数量积?什么是矢量积公式?平面向量数量积的坐标表示为:若a (x),向量的量积公式是什么?向量对应的量叫做量(物理学上叫标量),量(或标量)只有大小,没有方向。b公共起点处的夹角,很明显一个矢量的量积代表的是一个数,而不是一个矢量,b公共起点处的夹角,很明显一个矢量的量积代表的是一个数,而不是一个矢量。

平面向量数量积的坐标表示为:若a (x,y)和b (x,y),则a BX XY Y .给定两个非零向量a和b,则|a||b|cosθ(θ为a和b的夹角)称为a和b的定量积或内积,记为a B .两个向量的积等于其对应坐标的积之和量a b的乘积等于a |a|的长度和b在a |b|cosθ方向上的投影的乘积。

它可以被想象成一个带箭头的线段。箭头指示矢量的方向;线段长度:表示向量的大小。向量对应的量叫做量(物理学上叫标量),量(或标量)只有大小,没有方向。在物理学和工程学中,几何向量更常被称为向量。很多物理量都是矢量,比如物体的位移,球撞墙对其施加的力等等。反之则是标量,即只有大小没有方向的量。一些与向量有关的定义也与物理概念密切相关,比如向量势对应的是物理学中的势能。

Vector的标积公式:a * b | a | b | cos θ a,其中B代表向量,θ代表向量A和B一起开始时的夹角。显然,向量的标量积代表的是一个数,而不是一个向量。一个向量和另一个向量在这个向量上的投影的乘积,前提是起始位置相同。给定两个非零向量a和b,那么|a||b|cosθ(θ是a和b的夹角)称为a和b的数量积或内积,记为a B,两个向量的乘积等于它们对应坐标的乘积之和。
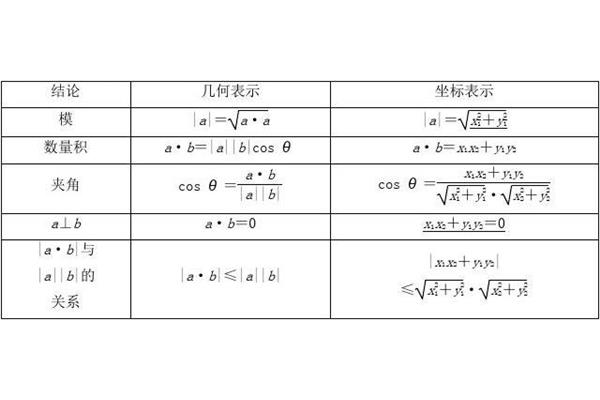
Y1),b(x2,y2),那么a.bx1.x2y1.y2向量的量积公式为:a * b | a | b | cos θ,B代表向量,θ代表向量A和B一起开始时的夹角。很明显,向量的量积代表的是一个数,而不是向量。一个向量和另一个向量在这个向量上的投影的乘积,前提是起始位置相同。扩展数据平面向量数量积给定两个非零向量A和B,那么|a||b|cosθ(θ是A和B的夹角)称为A和B的数量积或内积。
向量的标积公式:a * b | a | b | cos θ a,其中B代表向量,θ代表向量A和B一起开始时的夹角。显然,向量的标量积代表的是一个数,而不是一个向量。一个向量和另一个向量在这个向量上的投影的乘积,前提是起始位置相同。平面向量数量积 ①的几何意义如果一个向量在另一个向量方向上的投影是A和B之间的夹角,那么|b|cosθ称为向量B在向量A方向上的投影,而|a|cosθ称为向量A在向量B方向上的投影..

给定两个非零向量A和B,那么|a||b|cosθ(θ是A和B的夹角)称为A和B的定量积或内积,记为a B,两个向量的积等于它们对应坐标的积之和。即如果a (x1,y1)和b (x2,y2),那么a.bx1.x2y1.y2向量的量积公式为:a * b | a || b | cos θ,其中B代表向量,θ代表向量A和B在同一起点时的夹角。很明显,向量的量积代表的是一个数,而不是一个向量。
椭球方程:X/AY/BZ/C1 (A > 0,B > 0,C > 0)设椭球P (X,Y,Z)上有一点。椭球在P点的切面方程是X * X/AY * Y/BZ * Z/C1。考虑平面AX的一般方程,

矢量AB和矢量BC(注意不是CB)形成的角是∠B的外角,cos(AB,BC)cos(πB)cosB。如图所示。向量数量积的几何意义是:一个向量在另一个向量上的投影定义两个向量的数量积等于一个向量的模和另一个向量在这个向量方向上的投影的积,两个向量的数量积α和β α |||| β| cos θ其中| α|||| β|是两个向量的模θ和两个向量之间的夹角(0≤θ≤π)。如果有一个坐标α (0 ≤
Z1)β(x2,y2,z2)则αβx1 x2 y1 y2 Z1 z 2 |α| sqrt(x1 2 y1 2 z2)|βsqrt(x2 2 y2 2 z2 2)调用|b|cosθ向量b在向量A方向上的投影,所以两个向量之间的夹角可以通过量的乘积求出。
![{$DT[sitename]}](/skin/zx123/img/logo.png)