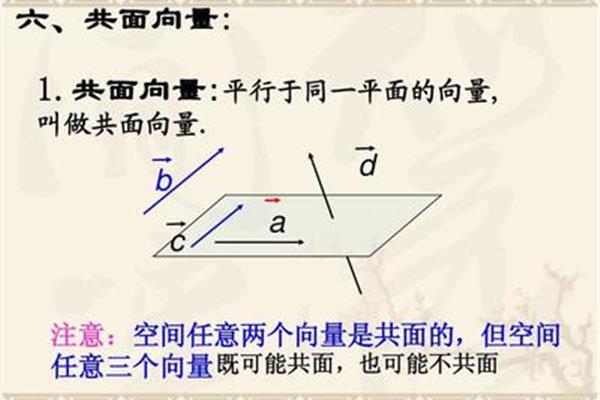
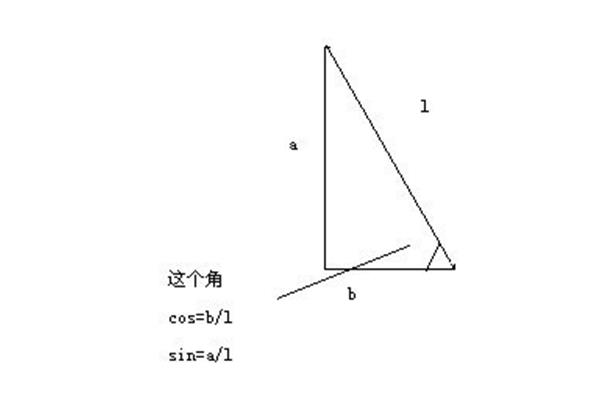
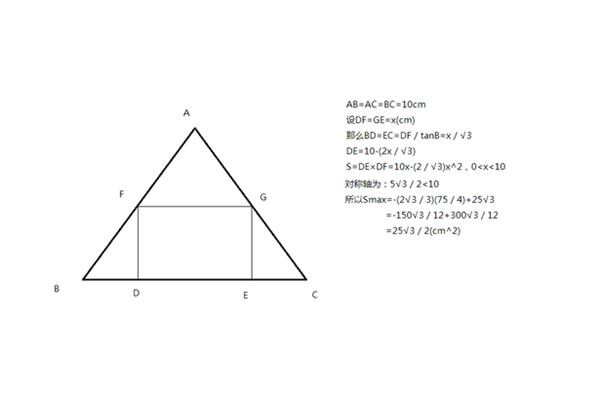
余弦定理公式推导 三角形正弦定理公式推导
正弦定理公式,余弦定理公式1,正弦定理公式a/sinAb/sinBc/sinC2R。正弦定理公式及其推论正弦定理:在三角形中,每条边的正弦与它所面对的角的比值相等,正弦定理和余弦定理的公式假设为任意三角形△ABC,角A、B、C的对边分别记为A、B、C,则正弦定理和余弦定理的公式及其推论如下。
两个角之和的正余弦公式:(1)sin(αβ)sinαcosβcosαsinβ;(2)cos(αβ)cosαcosβsinαsinβ;sin(αβ)cos(90°αβ)cos三角函数正弦定理公式为a/sinAb/sinBc/sinC2rD。正弦定理是三角学中的一个基本定理,指出“在任意平面三角形中,每边的正弦值与其对角线的比值相等,且等于外接圆的直径”。三角函数是角度的函数;它们在研究三角形、模拟周期现象和许多其他应用中非常重要。三角函数通常定义为包含这个角的直角三角形的两边之比,也可以等价定义为单位圆上各种线段的长度。

发展简史:从历史上看,正弦定理的几何推导方法丰富多彩。根据其思维特点,主要可以分为两种。第一种方法可以称为“等径法”,最早由13世纪的阿拉伯数学家和天文学家纳赛尔·丁和15世纪的德国数学家雷乔蒙塔努斯采用。“等径法”把三角形的两个内角的正弦看作半径相同的圆上的正弦线(16世纪以前,三角函数被看作线段而不是比值),利用相似三角形性质,使两者之比等于角的对边之比。

变形公式:在△ABC中,若角A、B、C的边为复数A、B、C,三角形的外接圆半径为R,利用正弦定理进行变形系统,包括a2RsinA、b2RsinB、c2RsinC(齐次化简)、asinBbsinAbsinCcsinBasinCcsinA,a:b:bsinA:sinB:sinC .TheLawofSines是三角学中的一个基本定理,它指出“在任意平面三角形中,每边的正弦值与它的对角线之比等于且等于外接圆的直径”,即a/sinAb/sinBc/sinC2rD(r为外接圆的半径,D为直径)。

正弦定理概述a/sinAb/sinBc/sinC2R正弦定理(1)已知三角形的两个角和一个边,求解三角形(2)已知三角形的两个边和一个边的对角,求解三角形(3)利用A: B: C Sina: SINB: SINC求解角度之间的换算关系;直角三角形的一个锐角的对边与斜边之比称为这个角的正余弦定理。余弦定理是揭示三角形各角之间关系的重要定理。可直接用于求解已知三角形的第三边或已知三边的夹角问题。如果对余弦定理进行修改,适当地移到其他知识中,使用起来会更加方便灵活。

正弦定理,三角形面积公式的正弦定理:在一个三角形中,每条边与其对角线的正弦之比相等,且都等于该三角形外接圆的直径,即a/sinAb/sinBc/sinC2R。面积公式:s △ 1/2bcsina1/2abcinc 1/2acsinb。1.正弦定理的变形及应用。
SinCc/2R。应用(1)利用正弦定理和三角形内角和定理,可以解决以下两类斜三角形问题:a .已知两个角和任意一条边,求另外两条边和一个角;b .已知两条边和一条边的对角线,求另一边的对角线。一般来说,知道两个边和一个边的对角线,就有两个解和一个解。(2) Sincc定理,它可以用来判断三角形的形状。它的主要功能是实现三角形中拐角关系的转换。比如判断三角形的形状时,A、B、C常分别用2RsinA、2RsinB、2RsinC代替。2.余弦定理在△ABC中,有a2 B2 c 22 bcco sa;B2C 2 a 22 acco sb;c2a .

设任意三角形△ABC,角A、B、C的对边分别记为A、B、C,则正弦定理和余弦定理的公式及其推论如下。正弦定理公式及其推论正弦定理:在三角形中,每条边的正弦与它所面对的角的比值相等。正弦定理公式,余弦定理公式1,正弦定理公式a/sinAb/sinBc/sinC2R。【注1】其中“R”为三角形外接圆的半径△ABC。下同。
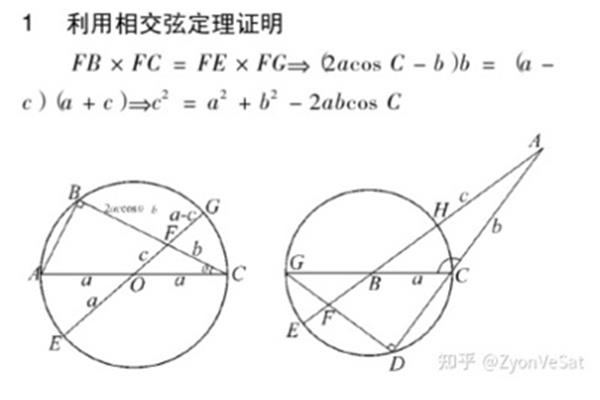
初中数学中,三角形内角的正弦值等于“对比角”,只适用于直角三角形。二、正弦定理推论公式1、(1)a2 rsina;(2)B2 rsinb;(3)c2RsinC .2 、( 1)a:bsinA:sinB;(2)a:csinA:sinC;(3)b:csinB:sinC;(4)甲:乙:辛那:辛那:辛那.【注意】常用于“边”和“角”的相互转换。

正弦定理:设三角形的三条边为abc,它们的对角为ABC,外接圆半径为R,则关系式a/sinAb/sinBc/sinC称为正道弦定理。余弦定理:设三角形的三条边为abc,它们的对角为ABC,那么这个关系叫做:A 2b 2c 22bc * COSA。b^2c^2 a^22ac*cosB。c^2a^2 b^22ab*cosC。

1。三角形正弦定理的证明:第一步。设三边为锐角的A、B、C△ABC。设CH⊥AB的竖脚为点HCHA SINBCHB SINA ∴ A SINBB SINA得到a/sinb/sinb。同理,在△ABC,b/sinBc/sinC步骤2。证明a/sinAb/sinBc/sinC2R:如图,任意三角形ABC都是ABC的外接圆。
8、正弦定理公式正弦定理的公式为:a/sinab/sinbc/sinc2R。正弦值是直角三角形中对边的长度大于斜边的长度的值,任意锐角的正弦值等于其余角的余弦值,任意锐角的余弦值等于其余角的正弦值。通常用符号sin表示,Sinθ也可以理解为顶角为θ的单位等腰三角形的面积与单位等腰直角三角形的面积之比。
![{$DT[sitename]}](/skin/zx123/img/logo.png)