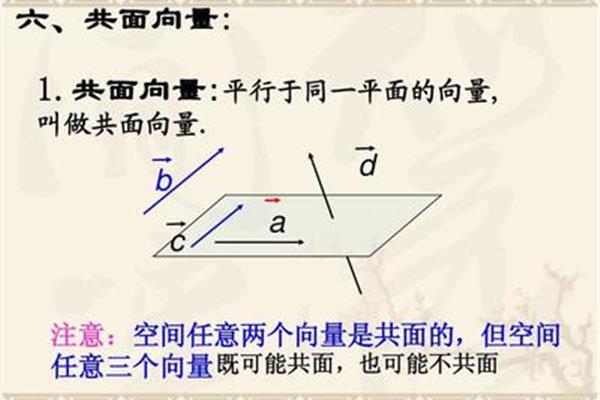
关于平面向量数量积的几个概念问题，在线性代数中抽象出了几何向量的概念，得到了更一般的向量概念平面向量数量积的几何意义是:一个向量在另一个向量上的投影定义了两个向量的数量积等于一个向量的模与另一个向量在这个向量方向上的投影的乘积；两个向量α和β | α| * | β| cos θ的量积，其中| α||| β|是两个向量的模θ和两个向量之间的夹角(0≤θ≤π)。

方向向量的定义是什么介绍如下:给定一条斜率为k的直线L，向量m(1，k)与直线L共线，与直线L共线的非零向量m称为直线L的方向向量..Directionvector是一个数学概念。空间中直线的方向用一个与直线平行的非零向量来表示，这个向量叫做直线的方向向量。空间中直线的方向用一个与直线平行的非零向量来表示，这个向量叫做直线的方向向量。

给定固定点P0(x0，y0，z0)和非零向量v{l，n}，确定通过点Pο并平行于V的直线L。因此，点P0和V是确定直线L的两个元素，V称为L的方向向量..因为对向量的模长没有要求，所以每条直线有无数个方向向量。直线上的任何矢量都平行于直线的方向矢量。扩展数据1。坐标表示:在平面直角坐标系中，取与X轴和Y轴方向相同的两个单位向量I和J作为一组基。

平行四边形法则:该法则通常表示为:做一个平行四边形，用表示两个向量的有向线段作为邻边，两个邻边之间的对角线表示两个向量之和。三角形法则:平移两个向量中的一个，使其首尾相连，然后用一条有向线段与两个向量相连，形成三角形，第三条边为合成向量。三角形法则和平行四边形法则的本质是一样的，都是矢量运算法则的表达。平行四边形法则:该法则通常表示为:以表示两个向量的有向线段为邻边构成平行四边形，两个邻边之间的对角线表示两个向量之和。

vector有平面向量和空间向量，有大小和方向，基本上是指两点之间的有向线段一般用线段名加“→”来表示，但很多书上都用粗体表示。向量是有方向的线段。它比一条线段多一个方向，线段的长度就是向量的模，也就是大小。表达向量时在线段上加个箭头就行了。在中学数学中，向量是二维和三维欧氏赋范空间R 2和R 3。在中学物理中，用向量来描述线性代数中的力、速度、动量的向量是一个抽象的概念，空间中具有线性结构的元素只要满足定义就称为向量。

向量有方向和大小，分为自由向量和固定向量。2.数学上只有大小没有方向的量叫量，物理学上叫标量。例如距离、质量、密度、温度等。第二，向量的大小，即向量的长度(或模数)。向量a的模数表示为|a|。1.向量的模是非负实数，大小可以比较。向量a(x，y)，| a | √( x ^ 2y ^ 2)。2.因为方向不能比较大小，向量也不能比较大小。

的(...高一数学。关于平面向量数量积的几个概念问题把,自己都凌乱了,求解释...

(2ab)的)只是一个括号，没有特别的意义。|...|2ab|的|表示这是向量的模关系，即(2ab)是向量(称之为向量c)，所以|2ab|是向量c的模，一个已知的向量可以找到它的模，但已知的模找不到原向量，因为模只是向量。()表示绑定关系，表示2ab是一个整体，就像1(2 ^ 3)和(12) 3一样。||代表模，是向量的长度，也可以理解为绝对值，但他的定义是| a |(a * a)(1/2)；

垂直和平行向量的公式是:如果A和B是两个向量:A = (x，y) B = (m，n)。那么a⊥b的充要条件是一个b0，即(xm yn)0。向量并行的公式为:a//b→a×bxnym0。在数学中，矢量是指有大小和方向的量。它可以被想象成一个带箭头的线段。箭头指示矢量的方向；线段长度:表示向量的大小。向量对应的量叫做量(物理学上叫标量)，量(或标量)只有大小，没有方向。

这里，向量被定义为向量空间的元素。需要注意的是，这些抽象向量不一定用数对来表示，大小和方向的概念也不一定适用。所以在平日阅读时，需要根据上下文来区分文章中提到的向量是哪个概念。但是，我们仍然可以找到一个向量空间的基来设置坐标系，我们也可以通过选择一个合适的定义来定义向量空间上的范数和内积，这使得我们可以将抽象的向量与具体的几何向量进行比较。

vector(英语:向量、物理、工程等。)是数学、物理、工程等许多自然科学中的一个基本概念。指既有大小又有方向，满足平行四边形法则的几何对象。向量记法:用粗体字打印字母(如A、B、U、V)，书写时在字母顶端加一个小箭头“→”。如果给定了向量的起点(a)和终点(b ),向量就可以记为AB(并加到顶部→)。

3)它是一个向量。在物理学和工程学中，几何向量更常被称为向量。很多物理量都是矢量，比如物体的位移，球撞墙对其施加的力等等。反之则是标量，即只有大小没有方向的量。一些与向量有关的定义也与物理概念密切相关，比如向量势对应的是物理学中的势能。几何向量的概念是在线性代数中抽象出来的，以得到更一般的向量概念。这里，向量被定义为向量空间的元素。需要注意的是，这些抽象向量不一定用数对来表示，大小和方向的概念也不一定适用。

向量数量积的几何意义是:一个向量在另一个向量上的投影定义了两个向量的数量积等于一个向量的模和另一个向量在这个向量方向上的投影的乘积， 以及两个向量α和β的量积||||||| β | cos θ其中| α||||是两个向量的模θ和两个向量之间的夹角(0 ≤θ≤ Y2，z2)那么αβX1 x2 YY 2 Z1 z 2 |α| sqrt(X1 2 y2z 1 2)|β| sqrt(x22 y2z 2 2)调用|b|cosθ向量b在向量A方向上的投影，所以利用量的积可以得到两个向量之间夹角的余弦

是，谁说不是？只是D点的位置不一样。等号表示矢量ab和dc方向相同，长度相等，平行或重合，记住向量有方向和长度。同样，向量abcd将点D的坐标设为(x，y)当向量abdc，so AB (1，2)，DC (3x，当向量abcd，设D点的坐标为(x。