三角函数性质什么事？反三角函数的性质反三角函数是基本的初等函数。锐角三角形的三角函数性质锐角三角函数1，锐角三角函数定义锐角a的正弦，三角函数的基本性质和定义是数学中一种常见的关于角度的函数，三角函数的定义和性质是什么？三角函数的性质是:三角函数是基本初等函数之一，它以角度为自变量，角度对应于任意角度终边与单位圆的交点的坐标或其比值为因变量。

(1)正弦函数和余弦函数的定义域都是实数集R，分别记为ysinx，x∈R，ycosx，x∈R，这里R当然可以改成(∞，∞)。(2)范围是因为正弦线和余弦线的长度小于或等于单位圆半径的长度。1 ≤ cosX ≤ 1。这说明正弦函数和余弦函数的值域都是1。知识点的定义和解释:三角函数sin(正弦)、COS(余弦)、tan(正切)是三角形中定义的比例关系。这些比例关系用于描述三角形的角和边之间的关系。正弦:在直角三角形中，正弦是指锐角的对边和斜边之比。正弦函数定义为对边/斜边的sinθ。余弦:在直角三角形中，余弦是指锐角的邻边与斜边之比。

正切(tan):在直角三角形中，正切是指锐角的对边与邻边之比。正切函数的定义是tanθ的对边/邻边。2.知识点的应用:三角函数的定义使其能够用于计算角和边的关系。利用三角函数，我们可以在已知三角形中任意两个值(角或边)的情况下，计算出其他未知值。3.知识点举例解释:问题:直角三角形中，已知一条直角边长为3，斜边长为5，求另一条直角边。

三角函数是数学中常见的一种关于角度的函数。也就是说，以角度为自变量，以角度与任意两条边的比值为因变量的函数称为三角函数，它将直角三角形的内角与其两条边的长度之比联系起来，也可以等价定义为与单位圆相关的各种线段的长度。三角函数在研究三角形、圆形等几何形状的性质中具有重要作用，也是研究周期现象的基本数学工具。在数学分析中，三角函数也被定义为无穷级数或特定微分方程的解，允许其值扩展到任意实值，甚至复值。

在航海、测量、工程等学科中，会用到其他三角函数如余切函数、割线函数、余切函数、正矢函数、半正矢函数等等。不同三角函数之间的关系可以通过几何直观或计算得到，称为三角恒等式。三角函数一般用于计算三角形中长度未知的边和角，广泛应用于航海、工程和物理中。另外，以三角函数为模板，可以定义一类类似的函数，称为双曲函数。

ysinx域:r；最大值为1，最小值为1，范围为[1，1]；周期为2π；在[0，2π]上的单调性是:在[0，π/2]上增加；它以[π/2，π]递减；在[π/2，π]处减小；在[3 π/2，2 π]中增加；F(x)sin(x)sin(x)f(x)奇函数ycosx域是实数r；范围[1，1]；最大值为1，最小值为1；

单调性在区间[π，0]内增加，在[0，π]内减少；Cos(x)cosx是偶函数ytanx {x丨x属于r，x≠π/2kπ，k属于z }；范围r；最小正周期为π；正切函数在每一个开区间(π/2kπ，π/2kπ)增加(k属于z)；这是个奇怪的函数。不好意思，我不知道什么是有界，书上也没找到，但希望以上知识对你有帮助。

三角函数的性质是:三角函数是基本的初等函数之一，它以角度为自变量，角度对应于任意角度的终边与单位圆的交点的坐标或其比值为因变量。也可以等效定义为与单位圆相关的各种线段的长度。三角函数在研究三角形、圆形等几何形状的性质中具有重要作用，也是研究周期现象的基本数学工具。在数学分析中，三角函数也被定义为无穷级数或特定微分方程的解，允许其值扩展到任意实值，甚至复值。

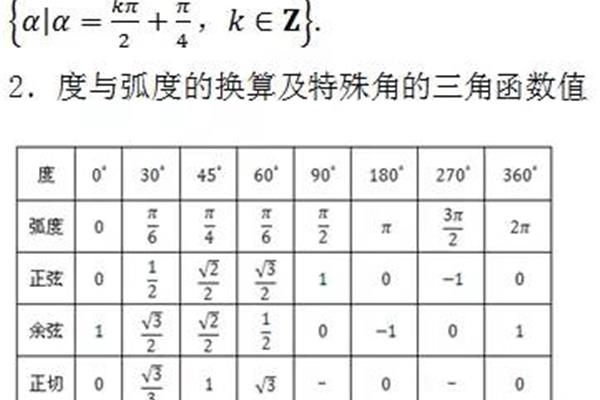
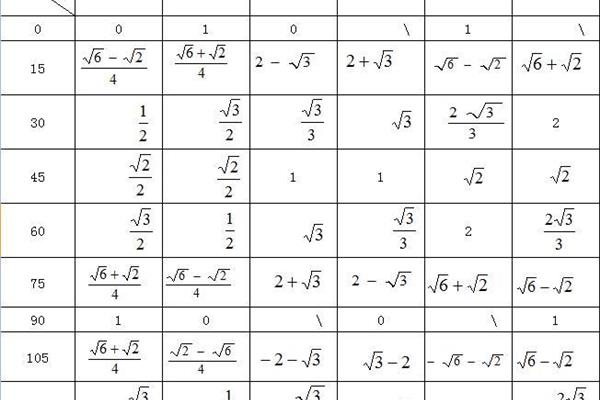
图像和三角函数性质的知识点如下:1。周期函数的定义:对于涵yf(x)，如果有一个非零常数T，使得f(xT)f(x)经常出现在X取定义域内的每一个值时，那么涵yf(x)称为周期函数，非零常数T称为这个函数的周期。2.正弦函数ysinx，x∈锐角三角函数1。锐角三角函数定义锐角A. 2的正弦、余弦和正切。补角三角函数之间的关系。sin(90°α)cosα，cos(90°α)sinα，tan(90°α)cotα，cot(90°α)tanα. 3、同角三角函数的关系:平方关系:sin2α cos2α1倒数关系:cotα(或tan α cotα 1)商:。

反三角函数是基本的初等函数。它是对arcsinx、反余弦arccosx、反正切arctanx、arccotx、arcsecx和arccscx的函数的统称，分别表示它们对x的反正弦、反余弦、反正切、反余切、反正切和反余切角，正弦和余弦函数的定义域为[1，1]，反正切和反余切函数的定义域为(-∞、∞)。