中垂线定理是几何学中一个重要的定理，它指出：在任意四边形内，任意一条中垂线都会将四边形分成两个相等的三角形。

中垂线定理的历史可以追溯到古希腊时期，当时古希腊数学家凯撒·阿米尔尼就提出了这一定理。他认为，在任意四边形内，任意一条中垂线都会将四边形分成两个相等的三角形。他的这一定理被称为“中垂线定理”，也被称为“凯撒定理”。

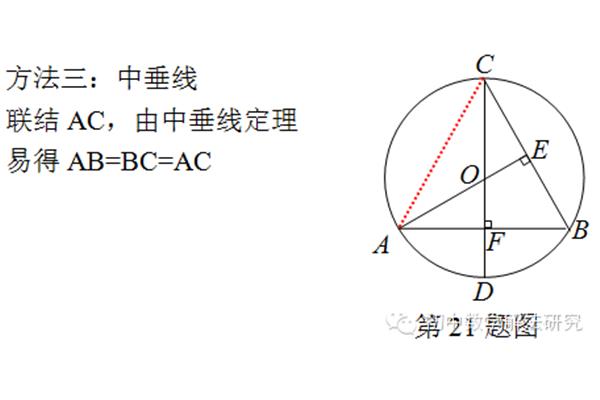
在中垂线定理的推导中，我们需要使用一些基本的几何定理，比如全等三角形定理、相似三角形定理等。

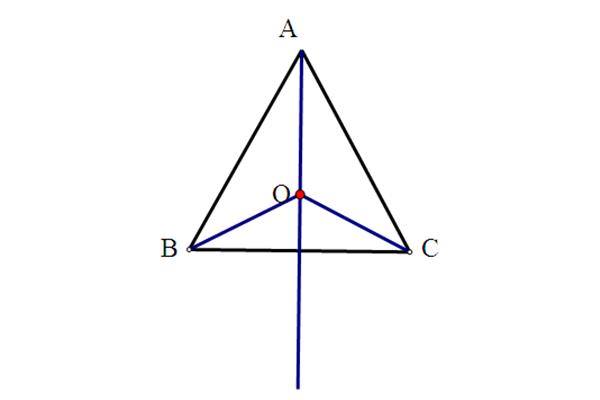
首先，我们假设任意四边形ABCD中有一条中垂线EF，将四边形ABCD分成两个三角形AEF和BDF，如图所示。

接下来，我们可以根据全等三角形定理，可以证明AEF和BDF是全等的，即它们的三条边长度和角度都是相等的。

最后，我们可以根据相似三角形定理，可以证明AEF和BDF是相似的，即它们的三条边长度相等，但角度不相等。

由此，我们可以得出结论：在任意四边形内，任意一条中垂线都会将四边形分成两个相等的三角形。

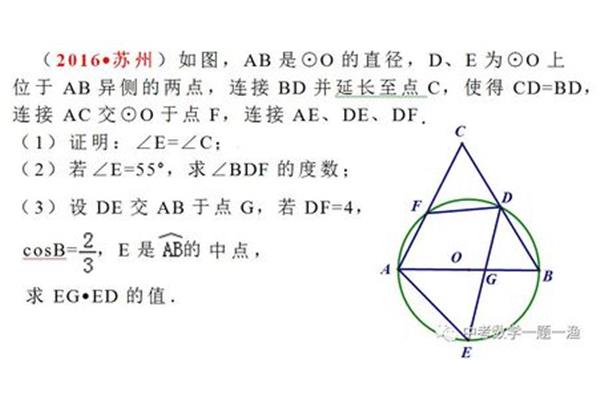
中垂线定理是几何学中的一个重要定理，它在许多几何学的应用中都有重要的作用。比如，它可以用来证明四边形内部的切线定理，也可以用来证明梯形的面积公式。此外，中垂线定理也与其他定理有着密切的联系，比如勾股定理等。

总之，中垂线定理是几何学中一个重要的定理，它在几何学的应用中也有着重要的作用。