二次函数的性质是什么？什么是一元二次函数性质？一元二次函数性质-0/二次函数yaxbx c (a ≠ 0)，当y0时，二次函数是关于x的一元二次方程，即axbxc0 (a ≠ 0)。此时，函数图像是否与x轴相交，就意味着方程是否有实根，二次函数的最高次一定是二次，二次函数的像是对称轴与Y轴平行或重合的抛物线，二次函数的最高次一定是二次，二次函数的像是对称轴与Y轴平行或重合的抛物线。

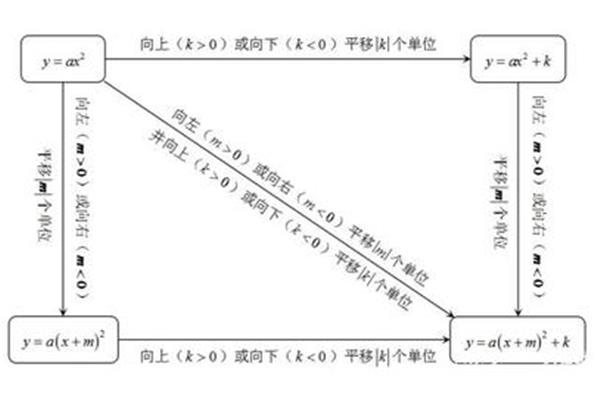
unary二次函数性质Yes:quadratic function的基本表达式是yaxbx c (a ≠ 0)。二次函数的最高次一定是二次，二次函数的像是对称轴与Y轴平行或重合的抛物线。二次函数的表达式为yaxbx c(且a≠0)，其定义为二次多项式(或单项式)。表情:1。当h>0时，将抛物线yax向右平行移动h个单位，可以得到ya (xh)的像。

3.当h > 0，k > 0时，将抛物线yax向右平行移动h个单位，再向上移动k个单位，即可得到ya (xh) k的像。4.当h > 0，k > 0时，将抛物线yax水平向左移动h个单位，再向下移动k个单位，可以得到ya (x h) k的像。5.当h < 0，k > 0时，将抛物线yax向左平行移动|h|个单位，再向上移动k个单位，就可以得到ya (xh) k的像。

这个解析图像的顶点的坐标是(1，2)，所以剩下的a1b2只需要用x2代替即可。Yax开口方向:向上A > 0，向下A < 0顶点坐标:(0，0)对称轴:Y轴函数变化:(1)当A > 0x > 0时，Y随X增大而增大；当x < 0时，y随着x的增加而减小。(2)当a < 0x > 0时，y随着x的增大而减小。当x < 0时，y随x的增大而增大.很大(最小)值:(1)当a > 0时，当x = 0时，y为最小值= 0。(2)当a < 0，x = 0时，y很大= 0。

对称轴是直线xb/2a。对称轴和抛物线的唯一交点是抛物线的顶点p。特别是当b0时，抛物线的对称轴是Y轴(即直线x0)。2.抛物线有一个顶点P，坐标为P(b/2a，(4acb 2)/4a)。当b/2a0时，p在Y轴上。当δb 24ac 0时，p在x轴上。3.二次系数A决定了抛物线的开口方向和大小。当a > 0时，抛物线向上张开；当a < 0时，抛物线向下打开。

二次函数一、定义和定义表达式一般来说，自变量X和因变量Y之间有如下关系:Yax 2bxc (a，b，c为常数，a≠0，a决定函数的开方向。当a>0时，开口方向向上，a0时，抛物线开口向上；A0，其中图像与X轴相交于两点:([b √δ]/2a，0)和([b √δ]/2a，0)；δ0，图像与X轴相交于一点:(b/2a，0)；。