-0的证明-0的证明简述如下。如何证明切线长定理？圆的切线定理是什么？一条直线l在点A∴l⊥OA处相切⊙O(切线性质定理)推论1过圆心且垂直于切线的直径必过切点推论2过切点且垂直于切线的直线必过圆心切线长定理定理从圆外的一点引出圆的两条切线，a点在⊙O ∴直线l。

1。圆心角定理:在同一圆或同一圆内，等圆心角有等弧、等弦、等弦心距。推论:在同一圆或同一圆内，若两个圆心角、两个圆弧、两个弦或两个弦的弦心距中的一组量相等，则对应的另一组量也相等。2.圆周角定理:与圆弧相对的圆周角等于与之相对的圆心角的一半。推论1:同弧或等弧的圆周角相等；在同一圆或同一圆内，相等的圆周角对应的圆弧也相等。推论二:半圆(或直径)对应的圆周角是直角；从圆周角90°推断:如果三角形一边的中线等于这条边的一半，那么这个三角形是直角三角形。3.垂直直径定理:垂直弦的直径平分弦，并平分弦所对的两个弧。

切线与性质切线的判定定理通过半径外端并垂直于该半径的切线为圆。几何语言:∵l⊥OA，a点在⊙O ∴上切线l在⊙O(切线判断定理)切线的性质定理圆的切线垂直于通过切点的半径。几何语言:∵直线l在点A∴l⊥OA处相切⊙O(相切性质定理)推论1过圆心且垂直于切线的直径必过切点推论2过切点且垂直于切线的直线必过圆心切线长定理定理从圆外的一点引向圆的两条切线

几何语言:∵弦PB，PD切线⊙O在a和c处∴PAPC,∠APO∠CPO( 切线长定理)弦切角定理弦切角等于它所夹圆弧对的圆周角。

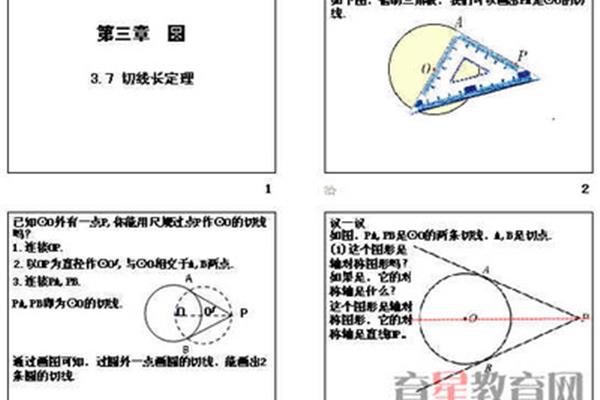
切线长定理其他几个结论可以直接用。用的时候要用切线长定理来说明。只有利用切线的性质才能做到。角度PAO角度PBO90度。因为角度BAC25是25度，所以角度AOB是18025 * 2130度。(等腰三角形AOB)。所以角P18013050度(四边形内角之和)。观察，猜测，证明，形成定理1。切线长度的概念:P是⊙O外的一点，PA和PB是⊙O的两条切线，我们称线段PA和PB为点P到⊙O的切线长度，从而引导学生理解切线和切线长度是两个不同的概念，切线是直线，不可测量；

tangent定理:若一条直线与圆上的一点P相切，则该直线的切线长度等于P点到圆心的距离。换句话说，切线等于半径。这个定理可以用数学符号表示为:PA⊥OP，其中PA代表切线的长度，OP代表从点p到圆心o的距离tangent tangent定理:如果两条切线在不同的切点a和b处与圆相交，则两条切线的交点c垂直于圆心o的连线OC..

TangentChordTheorem:如果一条直线在弦上与圆相交的切点A和点B同时与圆相切，那么切点A与弦上的点B之间的线段的平方等于这条直线与弦的两条线段的乘积。用数学符号表示:AB AC×AD，其中AB代表弦上切点A与点B之间的线段，AC和AD代表直线与弦的两段线段。

我觉得命题不一定成立。只要我们做一条与圆相交的线段，使得PO是它的中垂线，那么它们都满足PAPB。∠APO∠BPO，但是PA和PB不一定垂直于OA，OB就像:-0/的逆定理不成立，因为只要CD是直的，并且CD平行于AB，PAPB和∠APO∠BPO，这样的直线群就会是:PCPD，∠CPO∠DPO但是:OC⊥AP，OD