合理推理和演绎推理的数学问题如何证明？推理与证明1)定义:2 x ≠ 1，let 2 推理与证明数学上有什么区别推理与证明数学上有什么区别演绎推理(英文:演绎推理)是“结论、展开:。

教师要严格遵守逻辑规律，正确运用思维形式，做出示范，潜移默化地影响学生；其次，几何离不开图形。教学中要引导学生学会读图、画图、析图，正确理解图形，从图形中发现条件和结论，从而解决实际问题。第一，着重训练学生学会几何命题的除法。“话题设置”和“结论”命题由话题设置和结论两部分组成。有些命题有明显的结论。比如两条直线平行于第三条直线(题目设置)，那么这两条直线也是相互平行的(结论)。

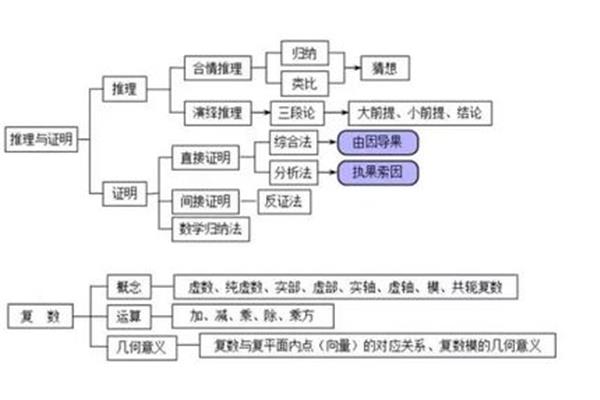
出现在高中新课标实验教材《数学(选修22)》一书中。合理推理和演绎推理是高中新课标实验教材(选修22)第二章第一节第一、二课时推理与证明。拓展:推理与证明 idea贯穿高中数学整个知识体系，对推理与证明的一般方法进行必要的总结和归纳，对后续的知识学习也有一定的指导作用。本章内容属于数学思想方法的范畴。把渗透到具体数学内容中的思维方法以集中而明确的形式呈现出来，可以提高我们的思维能力。

第一个方程是5090 60，第二个方程是565 60。因此，假设sin (X60)的平方是sin (X 60)的平方2/3。为了简单省略sin平方(X 60)的证明(sinX COS60)是SIN的平方(X60)。

1)定义域:2 x ≠ 1，x ≠ 0，f(x)x(2 x 1)/2(2 x 1)f(x)(2 x 1)/2(2 x 1)关于原点对称。显然√a √b>0(否则ab0与条件矛盾)∴√a√b(ab)/(√a √b)是一个有理数∴√asin 2 xcos 2(x 30)sin xcos(x 30)sin 2 xcos(2x 60)/21/。2 1/2 sinx *(cos xcos 30 sinxsin 30)sin2x cos2x/4 sin2x√3/4 1/2 sinxcosx *√3/2 sin 2 x/2 sin 2 x(12 sin 2 x)/4 sinxcosx *√3/2 1/2 sin 2 x/2 sin 2 x sin 2 x/2 1/4 1/2 sin 2 x cos 2(x 30)sinx cos(x 30)3/4

问题:设a(n ^ 1)x(根号21)*(an x)组合a12，a(n ^ 1)(根号21)*(an ^ 2)，n∈1，2，3，...解:x根号2，所以{根号2}是。

集合。