三角形是几何中最基本的形状，它由三条边组成，一般情况下，我们可以用三角形的三条边长来计算它的面积。这种方法叫做“海伦公式”，也叫做“海伦-秦九韶算法”，它是由古希腊数学家和几何学家海伦提出的。

海伦公式的公式是：

面积 = √（p ×（p-a）×（p-b）×（p-c））

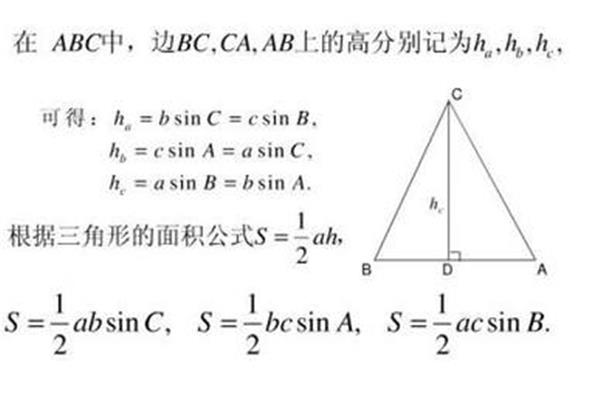
其中，a，b，c分别表示三角形的三条边，p表示三角形的半周长，即a，b，c的和除以2。

根据海伦公式，我们可以计算出任意三角形的面积。例如，如果一个三角形的三条边分别是a=3，b=4，c=5，则它的半周长p=（3 4 5）/2=6，那么它的面积就是：

面积=√（6×（6-3）×（6-4）×（6-5））=√（6×3×2×1）=6√3

因此，一个三角形的面积可以用海伦公式来计算。

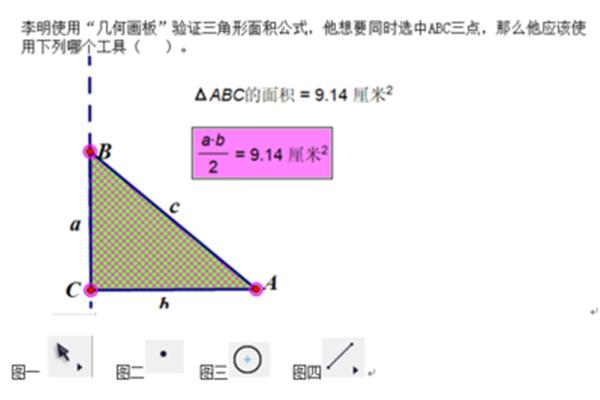
海伦公式不仅可以用来计算三角形的面积，还可以用来计算多边形的面积，只要将多边形分解成若干个三角形，然后把每个三角形的面积加起来，就可以得到多边形的面积。

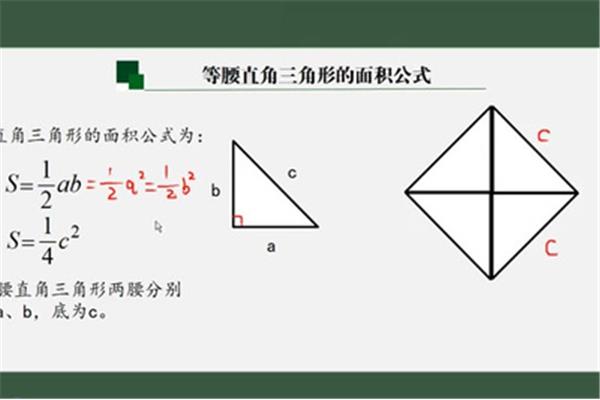
此外，海伦公式还可以用来计算三角形的角度，只要用三角形的三条边长来计算出它的面积，就可以用面积来求出三角形的角度。

海伦公式是几何中最基本的公式，它不仅可以用来计算三角形的面积，还可以用来计算多边形的面积和三角形的角度。它的计算过程非常简单，而且可以求出任意三角形的面积，因此被广泛应用于几何中。