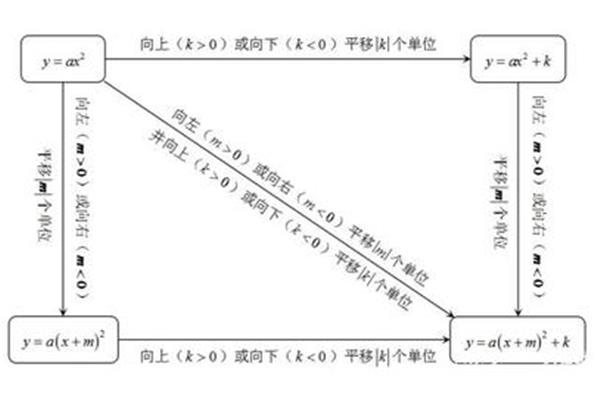
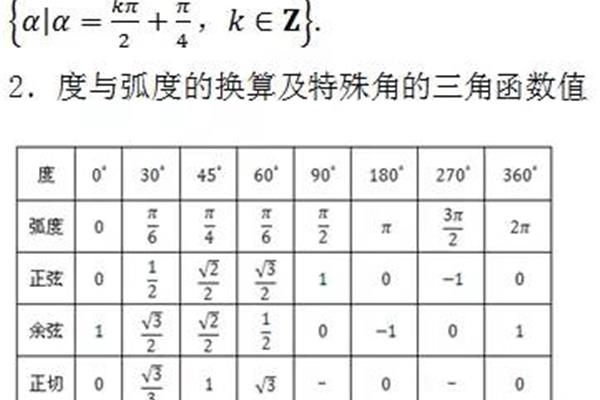
数学概念:函数的导数表示变化
函数的导数是数学中重要的概念,它表示一个函数在某一点的变化率。函数的导数是用来表示函数变化的量,它可以帮助我们研究函数的性质,如函数的极值、凹凸性、曲线的切线等。

函数的导数有很多种,比如常用的一元函数的导数、多元函数的导数、函数组合的导数、参数函数的导数、可微分函数的导数等。
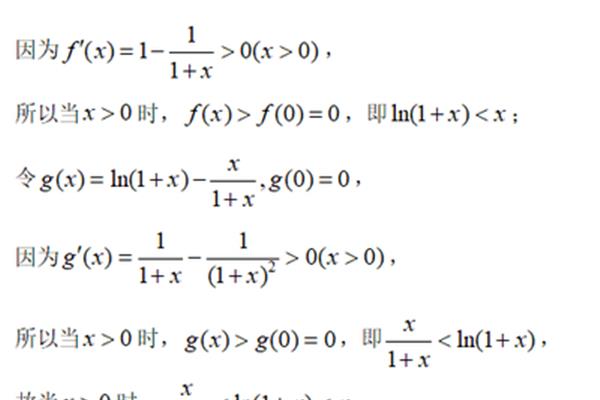
一元函数的导数是指一元函数的斜率,它可以用微积分的方法来求解,常用的求解方法有极限法、微分法和微分积分法。

多元函数的导数是指多元函数的偏导数,它可以用微积分的方法来求解,常用的求解方法有梯度法、极限法和微分积分法。

函数组合的导数是指函数组合的偏导数,它可以用微积分的方法来求解,常用的求解方法有链式法则、极限法和微分积分法。
参数函数的导数是指参数函数的偏导数,它可以用微积分的方法来求解,常用的求解方法有参数变化法、极限法和微分积分法。

可微分函数的导数是指可微分函数的偏导数,它可以用微积分的方法来求解,常用的求解方法有极限法、微分法和微分积分法。

函数的导数在微积分中有着重要的作用,它可以用来求解函数的极值、凹凸性、曲线的切线等,可以帮助我们更好地理解函数的性质。
函数的导数也可以用来解决很多实际问题,比如最小二乘法、最大似然估计、梯度下降法等,它们都可以用函数的导数来解决。

函数的导数也可以用来解决很多物理问题,比如力学中的力的定义、热力学中的能量定义、电动力学中的电场定义等,它们都可以用函数的导数来解决。
总之,函数的导数是一种重要的概念,它在微积分中有着重要的作用,它可以用来求解函数的性质、实际问题和物理问题,为我们解决问题提供了有效的方法。
![{$DT[sitename]}](/skin/zx123/img/logo.png)