导数基础知识教与学，包括导数的概念、导数的几何意义、基本初等函数的导数公式、导数的运算法则、复合函数的导数、导数运算的原则和方法、利用导数求切线方程的一般过程、导数与函数的单调性、导数与函数的极值、利用导数求函数的单调性，适合高二年级下学期教学使用，需要请转走。

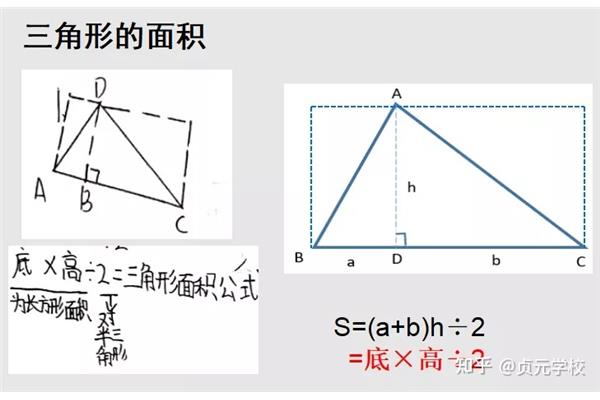
导数/:(u v) u v 的四种算法；(uv)‘u’v’；(uv) u v uv ；(u/v)(uvuv)/v^2。导数是函数的局部属性。函数在某一点的导数描述了该函数在这一点附近的变化率。如果函数的自变量和值都是实数，那么函数在某一点的导数就是函数在该点所表示的曲线的切线斜率。导数的本质是通过极限的概念对轴承数的局部线性逼近。

此时，函数yf(x)对于区间内x的每一个确定值都对应导数，构成一个新的函数，称为原函数yf(x)的导数，简称为y(x)，dv/dx或df(x)/dx。函数yf(x)在点x0的几何意义是导数f(x0):表示函数曲线在点PO(x0f(x0))的切线的斜率(-0/的几何意义是函数曲线在该点的切线斜率)。

1，C0(C是常数函数)。(x ^ n) NX(n1)(n∈q *)；记忆1/X of 导数。(sinx)cosx，(cosx)sinx，(e x) e x，(a x) (a x) lna (ln为自然对数)，(Inx)1/x(ln为自然对数)，(logax) x。

导数的计算已知函数的导函数可以根据导数的定义，利用变化率的极限来计算。在实际计算中，大多数常见的解析函数都可以看作是一些简单函数的和、差、积、商或互复合的结果，只要知道这些简单函数的导函数，就可以根据导数的求导法则计算更复杂函数的导函数。-0的求导法则/由基本函数的和、差、积、商或互复合而成的函数的求导函数，可由函数的求导法则推出。