多边形内角公式是一个对多边形内角求和的公式，它是一个重要的几何学公式，用于计算多边形内角的总和。它可以用来求解多边形的形状、大小、角度等。

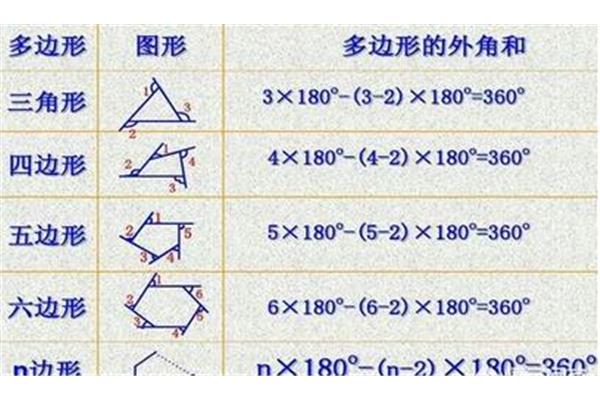
多边形内角公式是：S=180(n-2)，其中S表示多边形内角的总和，n表示多边形的边数。可以看出，当多边形的边数为3时，它的内角总和为180度；当多边形的边数为4时，它的内角总和为360度；当多边形的边数为n时，它的内角总和为180(n-2)度。

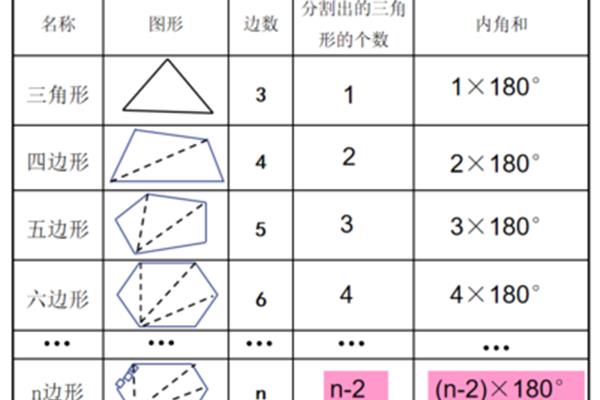
这个公式可以用来解决多边形的形状和大小问题。比如，当我们知道多边形的边数，可以用这个公式求出它的内角总和，从而知道它的形状。我们也可以用这个公式来求解多边形的大小。比如，如果我们知道多边形的内角总和，可以用这个公式求出它的边数，从而知道它的大小。

此外，多边形内角公式还可以用来求解多边形的角度。比如，如果我们知道多边形的边数和每个内角的度数，可以用这个公式求出多边形的总角度。

总之，多边形内角公式是一个重要的几何学公式，可以用来求解多边形的形状、大小和角度等问题。它的公式是：S=180(n-2)，其中S表示多边形内角的总和，n表示多边形的边数。