什么叫等腰三角形?什么三角形叫做等腰三角形？什么是等腰三角形？什么是等腰三角形？什么是等腰三角形？什么是等腰三角形？什么是等腰三角形？定义:两条边相等的三角形是等腰三角形。等腰确定等腰三角形，什么是等边三角形。

等腰三角形底边上的中垂线与两个腰的距离相等，一个腰的高度与等腰三角形底边的夹角等于顶角的一半。等腰三角形底边上任意一点到两个腰的距离之和等于一个腰的高度(需要用等面积法证明)，等腰三角形的腰长大于底边长的一半，小于周长的一半。Isoscelestriangle是指至少有两条等边的三角形，这两条等边称为这个三角形的腰。

等腰三角形的腰长于底边长度的一半，但小于周长的一半。等腰三角形底边上的中垂线到两个腰的距离相等，等腰三角形一个腰的高度与底边的夹角等于顶角的一半。等腰三角形底边上的任意一点到两个腰的距离之和等于一个腰的高度(用等面积法证明)。判断的定义方法:在同一个三角形中，两条边相等的三角形是等腰三角形。判定定理:在同一个三角形中，如果两个角相等，那么这两个角的对边也相等(简写为等角等边)。

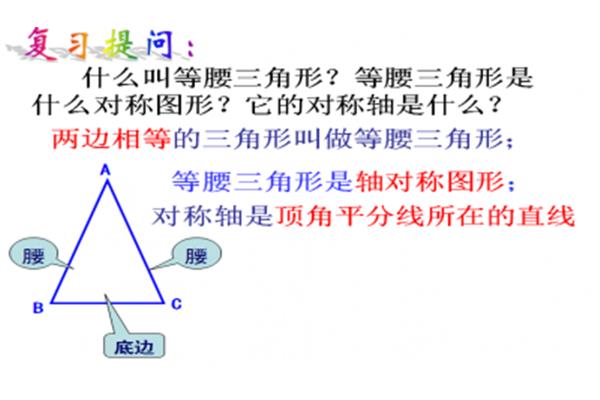
两条边相等的三角形叫做等腰三角形。定义二:有三条等边的三角形叫等边三角形，也叫正三角形。这是现行三年级数学教材中对上下两边的定义。我们从第一个定义可以理解，三角形的两条边相等，我们把这两条相等的边叫做腰，所以第三条边可能比腰长，也可能比腰短，三种情况下都可能等于腰。

所以这个三角形是两条边相等的三角形，也就是等腰三角形。因此，等腰三角形是一种特殊的等腰三角形。由此可以得出结论，他们的关系是一种属的关系。但是在三角形的分类上，如果按照角度分为三种，三角形有锐角、直角、钝角三种。

等腰三角形开放分类:三角形，几何定义:两条边相等的三角形是等腰三角形。等腰三角形的性质:等腰三角形的两个底角相等。等腰三角形的顶角平分线、底边上的中线和底边上的高度重合(简称“三条线合一”)，等腰三角形的两个底角平分线相等。(两腰中线相等，两腰高度相等)等腰三角形的底边到两腰的距离相等。等腰三角形的一个腰高与底边的夹角等于顶角的一半。等腰三角形的判断:有两个角相等的三角形。1.三角形任意两条边之和一定大于第三条边，这也可以证明三角形任意两条边之差一定小于第三条边。

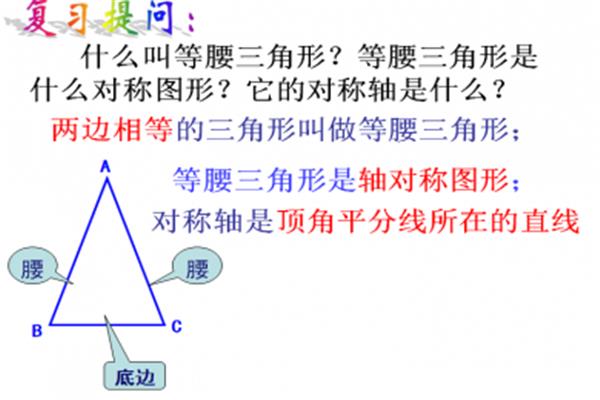
5、什么是等腰三角形?

isocelestriangle是指至少有两条等边的三角形，这两条等边称为三角形的腰。在等腰三角形中，两条相等的边叫做腰，另一边叫做底。两腰之间的夹角称为顶角，腰与底边之间的夹角称为底角。等腰三角形的两个底角相等(简写为“等边等角”)。一个角是钝角，两个角是锐角，是封闭图形。等腰三角形有两条相等的边，它与两边的夹角相等。

两个腰相等，两个底角相等。等腰三角形是指至少有两条等边的三角形。它的两条相等的边叫做这个三角形的腰，另一边叫做底。两腰之间的夹角称为顶角，腰与底边之间的夹角称为底角，两个底角的个数相等(简称“等边角”)，其余的角称为顶角。三角形的重心和垂心都垂直于顶点到底，等腰三角形可以分成两个全等的直角三角形。

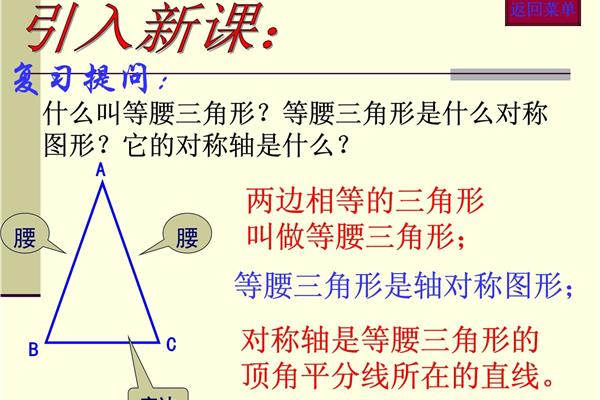
这样的三角形叫做等腰三角形，就是它的两条腰是一样的，长的那个叫做等腰三角形。三角形的三条边中有两条等长。这个三角形叫做等腰三角形。两条边相等的三角形叫做等腰三角形。等腰三角形是指至少有两条等边的三角形，这两条等边称为这个三角形的腰。在等腰三角形中，两条相等的边叫做腰，另一边叫做底。指至少有两条等边的三角形，两条等边称为这个三角形的腰。

等腰三角形是指至少有两条等边的三角形，这两条等边称为三角形的腰。在等腰三角形中，两条相等的边叫做腰，另一边叫做底。两腰之间的夹角称为顶角，腰与底边之间的夹角称为底角。等腰三角形的两个底角相等(简写为“等边等角”)。等腰三角形的面积公式(1)已知三角形的底为A，高为H，则Sah/2。(2)给定三角形的三条边A和C，那么(海伦公式)(p(a b c)/2)，Ssqrt定义:两条边相等的三角形是等腰三角形。等腰三角形的性质:1。等腰三角形的两个底角相等。(缩写为“等边等角”)2。等腰三角形的顶角平分线、底边上的中线、底边上的高度重合(简称“三条线合一”)3。等腰三角形两个底角的平分线相等。(两腰中线相等，两腰高度相等。) 4.等腰三角形底边的中垂线到两腰的距离相等。5.等腰三角形一腰高与底边的夹角等于顶角的一半。6.等腰三角形的判定:两条边相等的三角形是等腰三角形；两个角相等的三角形是等腰三角形(缩写为等边三角形)。1.三角形任意两条边之和必大于第三条边，由此可以证明三角形任意两条边之差必小于第三条边。

定义:两条边相等的三角形是等腰三角形。等腰三角形的顶角平分线、底边上的中线和底边上的高度重合(简称“三条线合一”)，等腰三角形的两个底角平分线相等，(两腰中线相等，两腰高度相等)等腰三角形的底边到两腰的距离相等。等腰三角形的一个腰高与底边的夹角等于顶角的一半，等腰三角形的判断:有两个角相等的三角形。1.三角形任意两条边之和一定大于第三条边，这也可以证明三角形任意两条边之差一定小于第三条边。