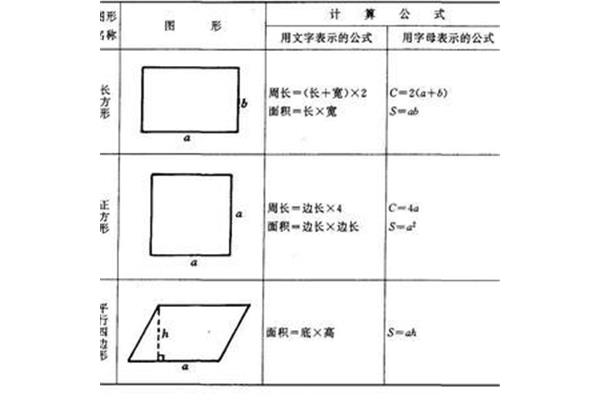
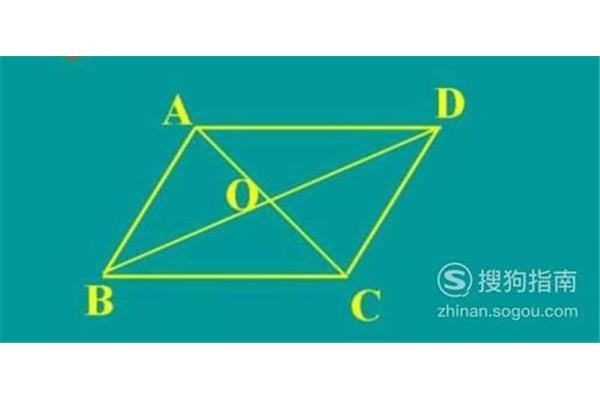
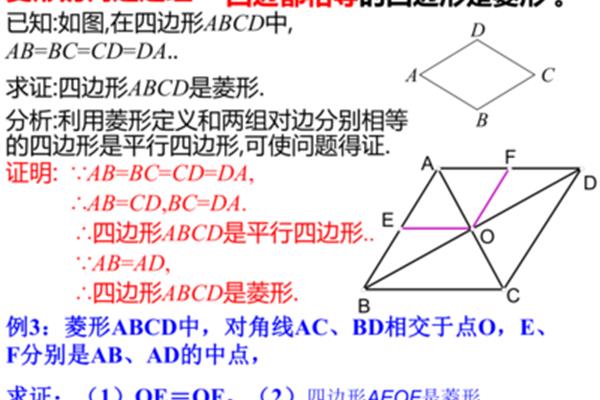
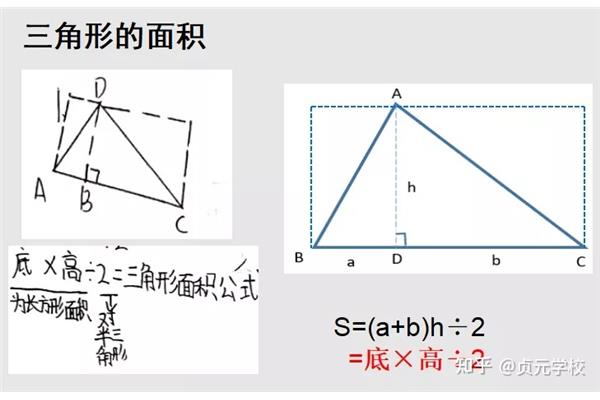
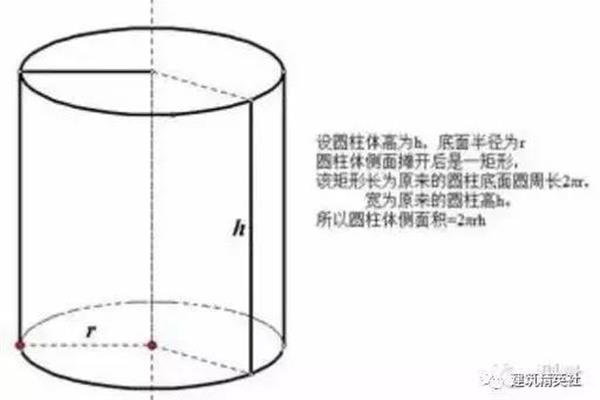
直角三角形对角线公式 等腰三角形对角线公式
等腰三角形的对角线没有公式三角形对角线公式。求多边形对角线的公式?任意凸多边形的外角之和等于360;多边形对角线的计算公式:N边形的对角线数等于1/2n(n3);如何计算对角线公式的对角线长度:d1.4142×a正方形的对角线计算方法如下:由于两个正方形的边与正方形的一条对角线构成直角三角形,所以可以利用勾股定理计算出正方形的对角线长度。
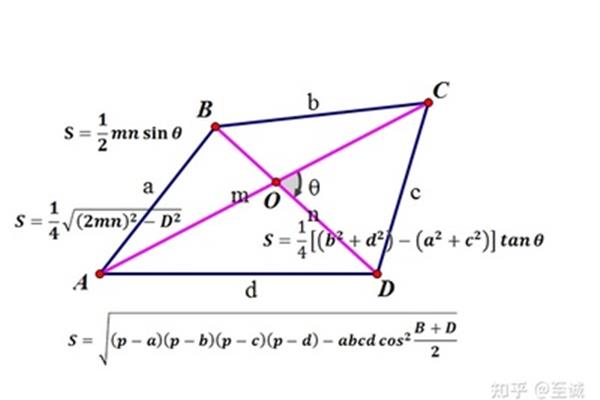
长方体的长、宽、高分别用A、B、C表示,所以底面对角线上有一个B,所以长方体是对角线√ A B C长方体的四条体对角线长度相等。只要证明一个体对角线的平方和及其长、宽、高的平方和设为A长A宽B高C和一个体对角线L .一个以长宽为边的矩形(rectangle)的对角线正方形A B在这个对角线和高体的对角线形成的三角形中,根据勾股定理就可以得到L (A B) Cabc的推广数据:特征:(1)长方体有6个面。
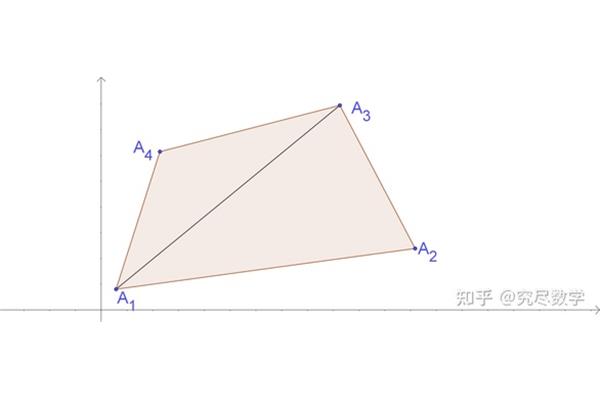
(2)长方体有12条边,四条对边的长度相等。根据长度,它可以分为三组,每组有4条边。(3)长方体有八个顶点。每个顶点连接三条边。长方体的三个棱叫做长、宽、高。(4)长方体的两条相邻边互相垂直。表面积等于相对的两个面,所以先数后面两个面,然后是前后面,最后是左右面。
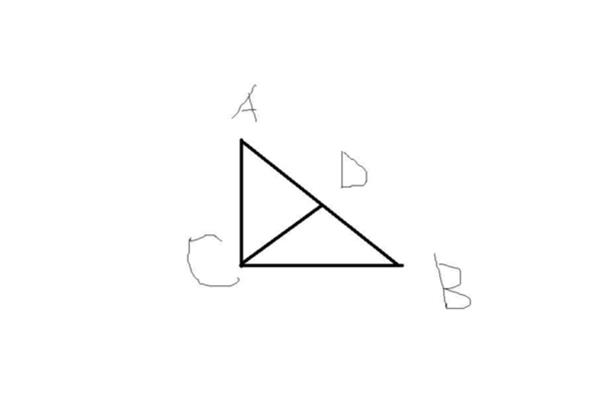
polygon的对角线公式是从一个N边形的顶点可以画出(n3)条对角线。N边形中有n(n3)/2条对角线。(n3)因为N边多边形有N条边,从一个顶点开始,除了这个顶点和它相邻的两个顶点不能是对角线之外,还有三条线,所以我们减去3得到(n3)。n(n3)/2是N(n3)因为从一个顶点可以画出(n3)条对角线,一个N边的多边形有N条边,但正好有一半是重复的,所以除以2就是N(n3)/2。
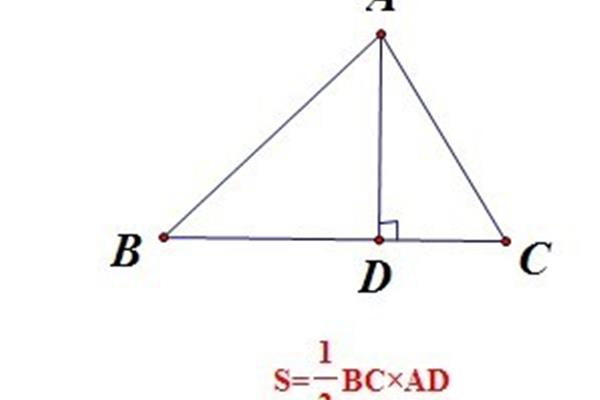
扩展资料:多边形其他公式:多边形内角之和:[N2 ]× 180证明:取N边形中的任意一点O,与每个顶点相连,将N边形分成N个三角形。因为这N个三角形的内角之和等于n 180,所以以O为公共顶点的N个角之和是360。所以N边形的内角之和是N ^ 180 ^ 2×180(N2)180。也就是说,N边形的内角之和等于(N2) × 180。
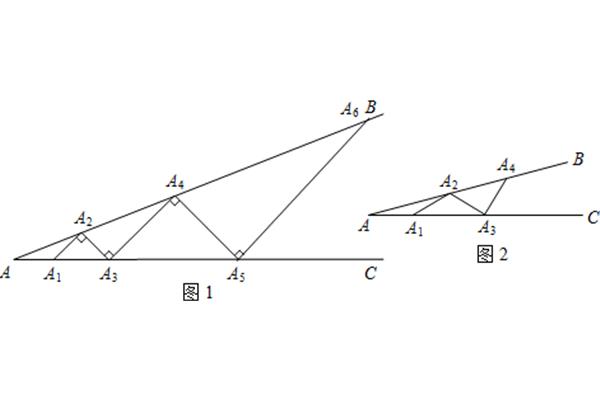
多边形的对角线公式:kn(n3)/2。组成多边形的线段至少有三条,三角形是最简单的多边形。组成多边形的每一条线段称为多边形的一条边;两条相邻线段的公共端点称为多边形的顶点;多边形的两条相邻边所形成的角称为多边形的内角;连接多边形两个不相邻顶点的线段称为多边形的对角线。任意凸多边形的外角之和等于360;多边形对角线的计算公式:N边形的对角线数等于1/2n(n3);
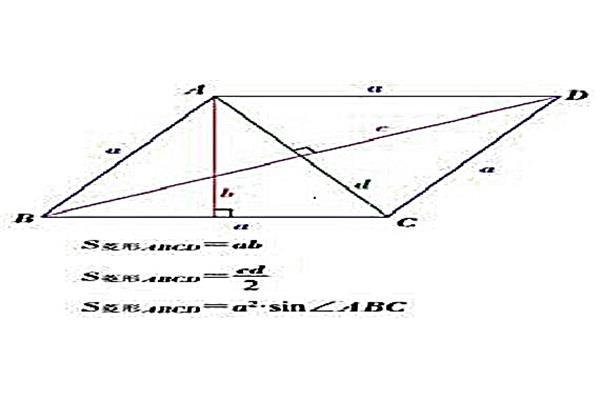
计算对角线长度的公式:d1.4142×a正方形的对角线长度计算如下:由于两个正方形的边与正方形的一条对角线构成直角三角形,所以可以利用勾股定理计算正方形的对角线长度。长度等于正方形边长的平方根的两倍。正方形的对角线和两边形成等腰直角三角形。如果正方形的边长是a,那么对角线的长度就可以根据勾股定理计算出来,对角线= √ 2a。
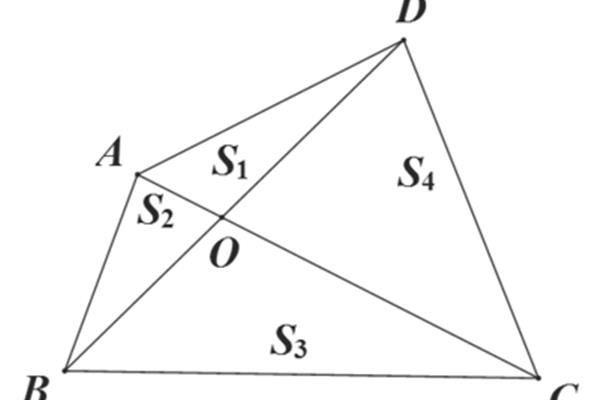
1两点之间只有一条直线。2两点之间最短的线段是3。同角或同角的余角相等。4.同角或同角的余角相等。5.只有一条直线垂直于已知直线。6.在直线上所有与点相连的线段中,垂直线段的最短平行公理通过直线外的一点,且只有一条直线与这条直线平行。8如果两条直线都平行于第三条直线,则这两条直线也相互平行。9.等腰角相等。两条直线互相平行。10.内部位错角相等。11.它们是相辅相成的。12.两条直线平行。等腰角相等。13.内部位错角相等。14.两条直线平行。同边内角的互补15定理三角形两边之和大于第三边16推论三角形两边之差小于第三边17三角形内角之和与定理三角形三个内角之和等于180 18推论直角三角形的两个锐角互补19 推论三角形的一个外角等于两个不相邻的内角之和20推论三角形的一个外角大于一个不相邻的内角的任何对应边21全等三角形,角公理(SAS)有两个角相等的三角形。 角公理(ASA)有两个角相等的三角形。推论(AAS)有两个角度相等的三角形。有两个角和一个角。
6、等腰 三角形对角线公式等腰三角形的对角线没有公式。等腰三角形至少有两条等边,这两条等边称为这个三角形的腰,在等腰三角形中,两条相等的边是腰,另一边是底。等腰三角形的两个底角相等(简写为“等边等角”),等腰三角形的性质:一般的等腰三角形是只有一个对称轴的轴对称图形,顶角平分线所在的线就是它的对称轴。但是等边三角形(一种特殊的等腰三角形)有三个对称轴。
![{$DT[sitename]}](/skin/zx123/img/logo.png)