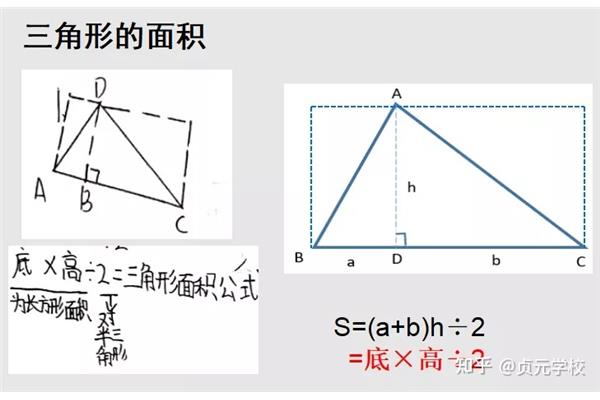
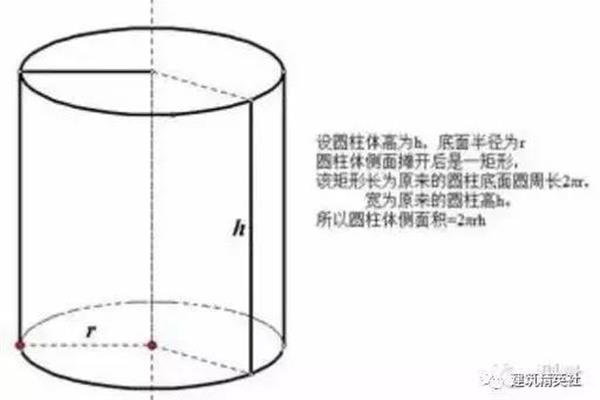
算术平均和等比中项公式,算术级数等比中项公式
等比例均值项。几何级数的一般公式。几何级数的判定首先是定义方法。相邻两项之比是常数,即公比q .二,中位数法。第三,通式法。如果满足几何级数的同项公式,则为几何级数。第四,前n项的求和公式法。如果前n项的求和公式与等比数列的求和公式一致,则为几何级数。几何级数的前n项和公式。

中项法:对于任意三个连续项,如果它们是几何级数,则中间项的平方等于两项的乘积。例如,等差数列的通项是用累加法得到的等差数列的前n项的和公式,几何数列的通项公式是用后向加法得到的,几何数列的前n项和是用错位减法得到的。第三章是数列5几何级数前n项及公式的推导。本文对豫北名校2024年高三数学高考试卷上的单项选择题题进行了分析。题目比较常规,主要考查等比项、余弦定理、基本不等式和面积公式。
别忘了几何级数的前n项和这个公式,非常有用。-几何级数的通项公式:对于几何级数an = a1 * r(n-1),其中an表示第n个数,a1表示一项,r表示公比。几何级数的概念和性质几何级数的定义几何级数是指每一项与其前一项的比值等于二项的相同常数的级数。几何级数。几何级数的一般形式是:a,
这个常数称为几何级数的公比,通常用字母Q表示..例如通过构造几何级数来解决某些不等式问题或利用几何级数的性质来解决函数的很大值问题。引言几何级数是高中数学中另一个重要的数列。与等差数列相比,它具有独特的性质和规律。在数学竞赛中的应用:在数学竞赛中,几何级数的知识点经常与其他知识点结合出现,如不等式和函数。
-等差数列通项公式:对于等差数列,an = a1(n-1)d,其中an表示第n个数字,a1表示一项,d表示容差。几何级数在实际问题中的应用:几何级数在实际问题中应用广泛,如计算复利和增长率。几何级数的概念。几何级数的判断。几何级数的任意两项之比是常数:即对于任意正整数M和N,有一个通式AM/AN = Q(M-N):AN = A1 * Q(N-1)求和公式:当q1,Sn = A1(1-Q N)/(1-Q)当q=1。
![{$DT[sitename]}](/skin/zx123/img/logo.png)