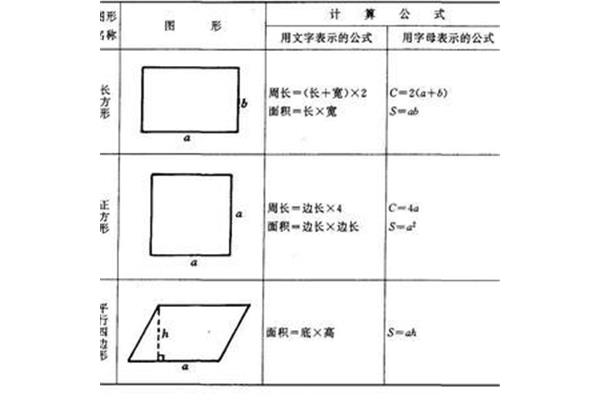
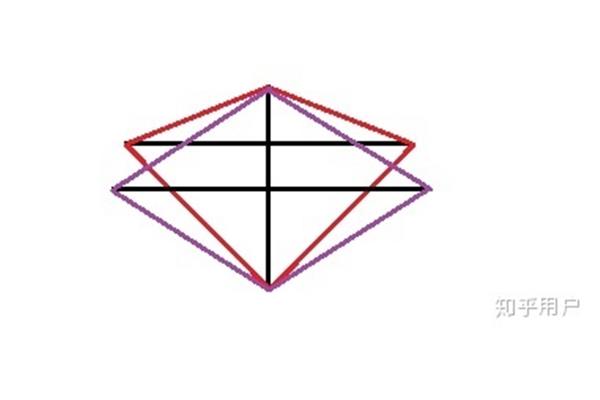
菱形是平行四边形?四种方法一
如何证明菱形的性质?如何证明钻石?你能证明它是钻石吗?有四种方法可以证明平行四边形是菱形。证明菱形对角线互相垂直的过程已知:四边形ABCD是菱形,对角线AC和BD相交于o点证明:AC⊥BD证明:∵ABCD是菱形,菱形是平行四边形,它们的对角线平分,如何证明菱形的面积等于它的对角线乘以菱形的对角线。
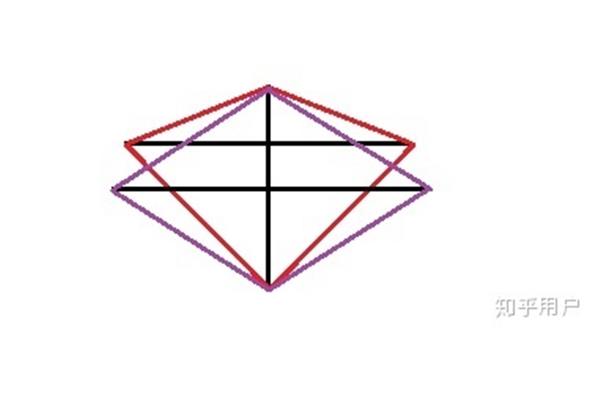
怎样证明菱形的面积等于其的对角线相乘
菱形的对角线互相垂直,菱形的面积是2*三角形的面积是2 * 1/2 * a * (b/2) 1/2 a * ba,b是对角线长度。根据平行四边形计算面积,如果发现与底等高,可以作为辅助线或者:菱形面积对角线的乘积除以2。菱形abcd的对角线ac,bd相交于点O,面积三角形abd面积三角形cbd面积BD * ao/2bd * co/2bd/2(aoco)BD/2 * acbd * AC/2。
四条边都相等,能证明是菱形吗?
是的,平面上一组相邻边相等的平行四边形是菱形,对角线垂直的平行四边形是菱形,四边相等的四边形是菱形。两组对边相等,所以是平行四边形。边长相等的平行四边形,所以是菱形。可以证明,有四条等边的四边形是平行四边形,平行四边形的两条相邻边是菱形。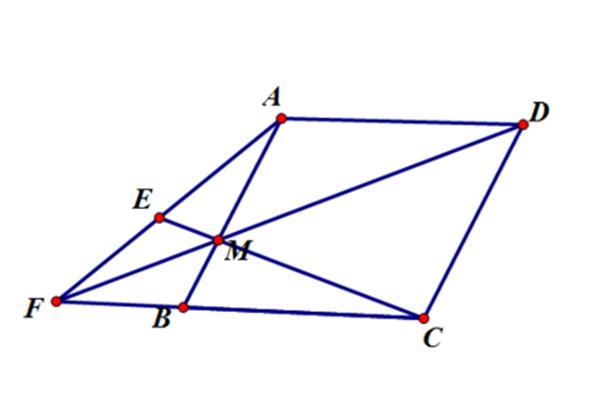
证明菱形对角线互相垂直的过程
已知四边形ABCD是菱形,对角线AC和BD相交于o点,证明:AC⊥BD证明:∵ABCD是菱形,对角线等分。∴AOCO∵ABBC So AC是等腰三角形ABD ∴AC⊥BD(三条线合一的等腰三角形)菱形中BD的中心线:在同一平面上,一组相邻边相等的平行四边形是菱形。四条边相等的四边形是菱形,或者一组相邻边相等的平行四边形是菱形。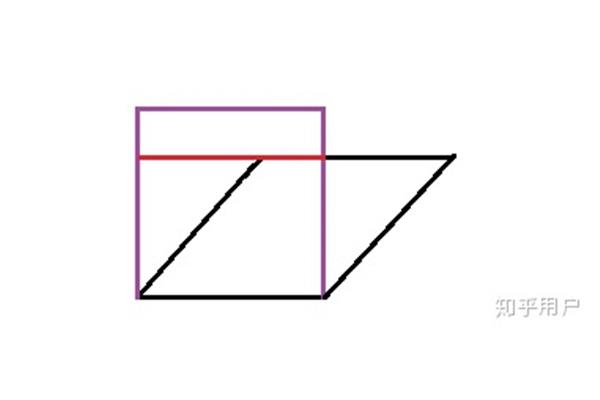
菱形具有平行四边形的所有特性;菱形的四个边都相等;菱形的对角线相互垂直平分每组对角线菱形是一个轴对称图形,有两个对称轴,即两条对角线所在的直线,菱形或中心对称图形菱形的面积等于两条对角线乘积的一半;当难以求出对角线长度时,用平行四边形面积的一般计算方法计算菱形面积S底×高菱形的特征:对角线互相垂直并平分,每条对角线平分一组对角线。
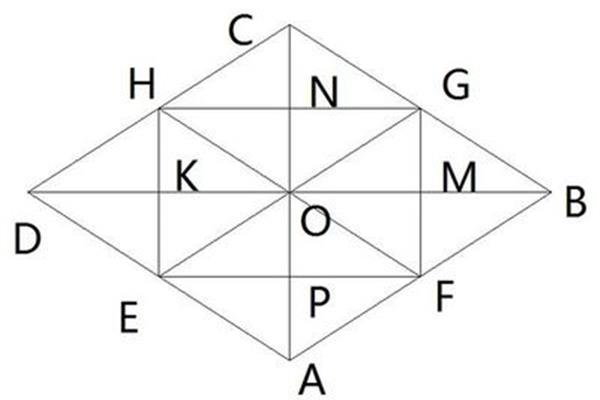
如何证明菱形的对角线互相垂直且每条对角线平分
已知:如图,四边形ABCD为菱形,对角线AC与BD相交于o .证明:AC⊥BD、AC、BD等分,一组对角线等分。证明:菱形ABCD是一个特殊的平行四边形∴OAOC,obod∶abcdcad∴AC⊥BD。设正方形ABCD的边长为a,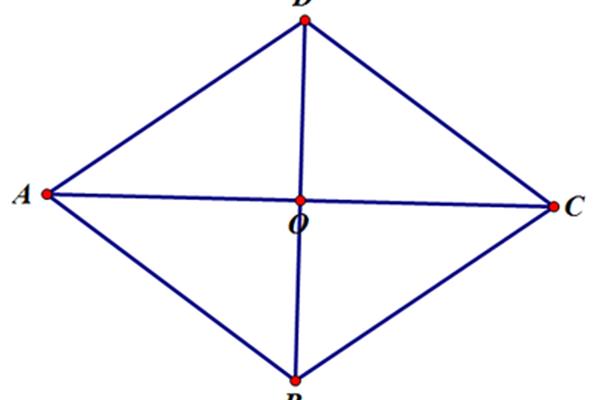
由勾股定理> A的对角线AC长度是根号的两倍,而A的对角线BD长度是根号的两倍。>对角线长度相等。三角形ABC是等腰直角三角形,>角CAB是45度。类似地,>角度ABD是45度。所以三角形ABO的两个角都是45度,也是等腰直角三角形。因此,(1)AC垂直于BD。(2)AOBO,同理,BOCO,CODO,> AC和BD可以垂直等分,而且因为刚刚证明了每个角都是45度,对角都相等。
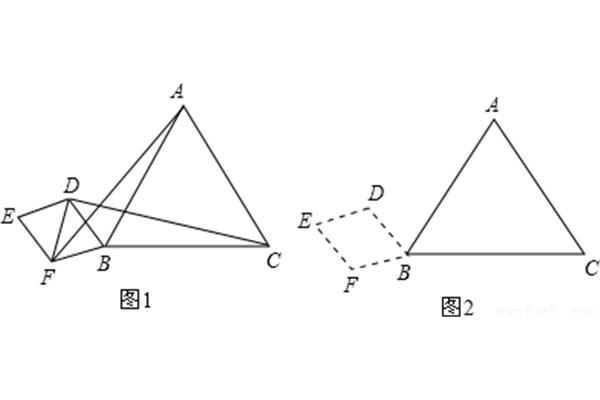
证明一个平行四边形是菱形的证明方法4种
方法1。一组相邻边相等的平行四边形是菱形。方法二。对角线互相垂直的平行四边形是菱形。方法三。对角线平分一组对角线的平行四边形是菱形。方法四。关于对角线对称的平行四边形是菱形。1.有四条等边的四边形是菱形。2.对角线互相垂直的平行四边形是菱形。3.一组邻边相等的平行四边形是菱形。4.对角线平分且互相垂直的四边形是菱形。1.四边是平等的。2.对角线垂直等分。3.一条对角线被等分成一组对角线。
方法一:一组相邻边相等的平行四边形是菱形。方法二:对角线互相垂直的平行四边形是菱形。方法三:对角线平分一组对角线的平行四边形是菱形。方法四:关于对角线对称的平行四边形是菱形。平行四边形的性质是:平行四边形的两组对边相等;(2)平行四边形的两组对角分别相等;(3)平行四边形的邻角是互补的;(4)平行四边形的对角线等分。
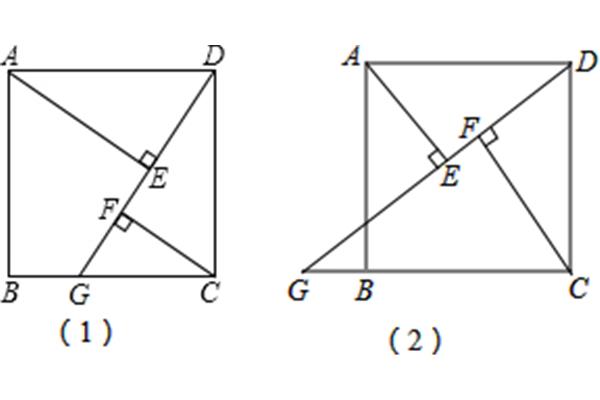
菱形怎么证明?
有两组对边平行且切角相等,但不是90度的四边形是菱形。你可以分别证明这三个条件。证明两组对边平行,四边等长。平面上一组相邻边相等的平行四边形是菱形,这是标准定义。证明方法如下:1。对角线互相垂直并平分,每条对角线平分一组对角线;2.四边都是平等的;3.对角相等,邻角互补。菱形具有平行四边形的所有性质,其他四边相等。两条对角线互相垂直,平分菱形。决定1。一组邻边相等的平行四边形是菱形。2.对角线垂直的平行四边形是菱形。3.四边相等的四边形是平行四边形。初三数学教案1.33节:菱形的性质定理证明教学目标:掌握菱形的性质判断,使学生灵活运用菱形的知识解决相关问题,提高能力。通过明确划分矩形和菱形的定义和性质,可以训练学生改正错误。教学重点:菱形的自然定理证明教学难点:自然定理的应用以及生活数学与纯数学的相互转化。如何证明菱形的性质??
![{$DT[sitename]}](/skin/zx123/img/logo.png)