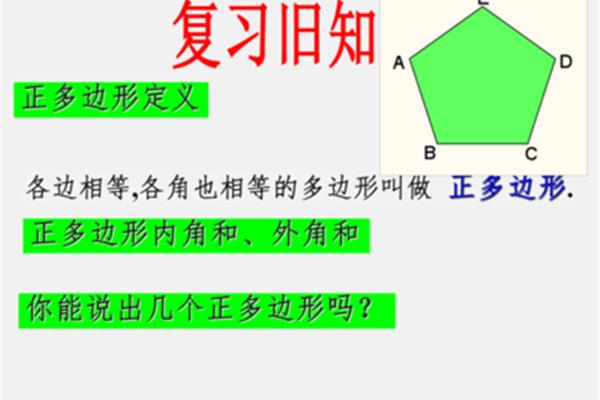
多边形定义:所有边都相等,矩形不一定是菱形
给定边数的正多边形是否可以几何作图?正多边形的边数与内角度数有什么关系?正多边形是一种具有相等边长和内角的多边形。在几何作图中,可以使用直尺和圆规来构建一些几何图形,但并不是所有的正多边形都可以通过几何作图来构造,今天在这里,我们就来讨论一下给了定边数的正多边形是否可以几何作图,并研究正多边形的边数与内角度数之间的关系。
每条边的长度相等,并且每个内角的度数也相等。我们用R表示正多边形的外接圆的半径,r表示内切圆的半径,d表示正多边形的对角线长度。对于正多边形是否可以几何作图的问题,这涉及到一个重要的数学概念,即可构造数。可构造数是指可以通过使用直尺和圆规进行有限步骤的加、减、乘、除、开方、求交等运算来构造的数。根据古希腊的尺规作图法则,只有可构造数的长度可以通过几何作图来构造。
positive 多边形-1/如下:positive多边形表示所有边都相等,所有角都相等多边形。尺子圆规量角器可以画任何正。本定义中的条件在所有方面都是平等的。角度也是对等的,“缺一不可”。如果菱形的边相等,则菱形不一定是正的多边形因为四个角不相等。正多边形的特征:正多边形的外接圆的圆心称为正多边形的圆心。正多边形的外接圆半径称为正多边形的半径。内切圆多边形的中心到两边的距离称为远点。
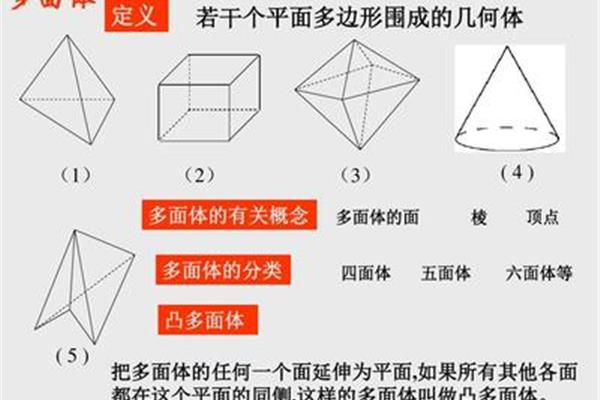
在正多边形中,可以用来展开一个中间没有缝隙的平面的只有三种,即正三角形、正方形和正六边形。因为正三角形的每个角等于60度,所以当六个正三角形放在一起时,公共顶点上的六个角之和等于360度。正方形的每个角等于90度,所以当四个正方形放在一起时,公共顶点的四个角之和正好等于360度;正六边形的每个角等于120度。当三个正六边形放在一起时,公共顶点处的三个角之和也等于360度。
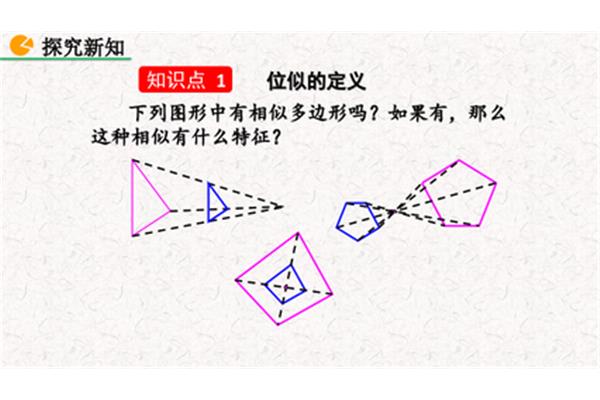
这个问题是一个开放性问题,没有说明用什么标准来分类多边形!比如根据多边形的边数,可以分为:三边形、四边形、五边形;根据边长是否相等,可分为:等边多边形,不等边多边形等等;按角度的大小可分为等角多边形和不等角多边形等等。按其形状的凹凸程度,可分为凹多边形和凸多边形等。当然,还有很多不同的分类方法。
在数学中,由三条或三条以上线段首尾相连组成的平面图形称为多边形。根据标准的不同,多边形可分为正多边形和负多边形、凸多边形和凹多边形,中文名多边形mbth polygon定义有三条线且三条线以上的图形属性为正的图形关键字多边形,space 多边形应用数学概念多边形在同一平面上。
![{$DT[sitename]}](/skin/zx123/img/logo.png)