等比数列是数学中常用的一种数列，它的特点是每一项都是上一项的一个常数倍。等比数列的公式为。

an=a1*q^(n-1)

其中，a1表示等比数列的第一项，q表示等比数列的公比，n表示等比数列的项数。

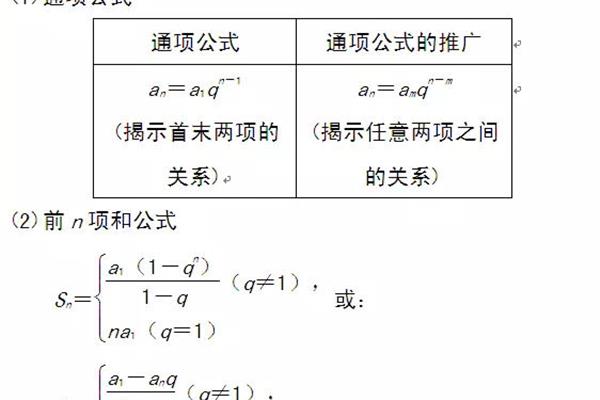
等比数列的公式是由等比数列的性质来推导出来的，它可以用来求解等比数列的任意一项。

例如，已知等比数列的第一项是2，公比是3，求第五项的值，则可以用等比数列的公式来求解，即a5=2*3^(5-1)=2*3^4=2*81=162。

此外，等比数列的公式还可以用来求解等比数列的和。例如，已知等比数列的第一项是2，公比是3，求前10项的和，则可以用等比数列的公式来求解，即Sn=a1*(1-q^n)/(1-q)=2*(1-3^10)/(1-3)=2*(1-59049)/(-2)=2*29525=59050。

等比数列的公式是非常实用的，它可以用来求解等比数列的任意一项，也可以用来求解等比数列的和。因此，等比数列的公式在数学中有着重要的应用价值。