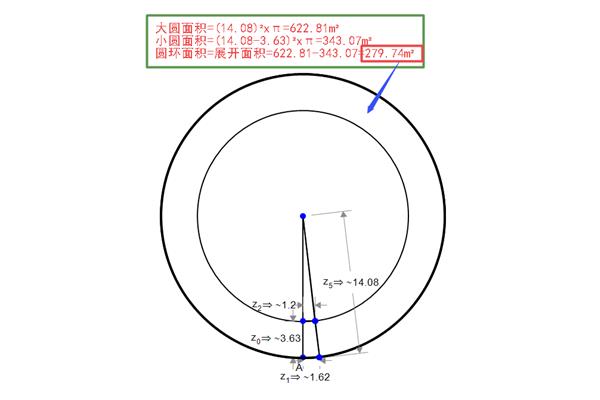
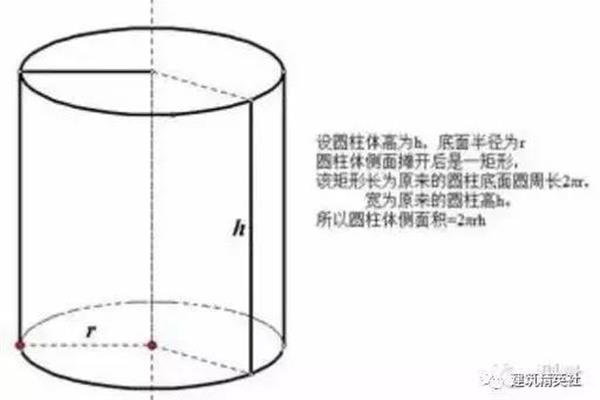
圆的面积和周长的计算公式?如何计算圆的周长?
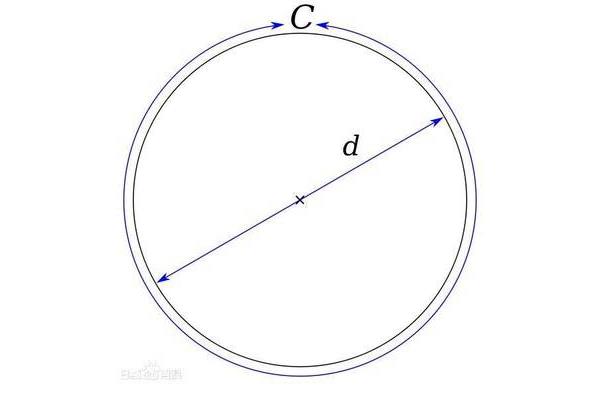
目前圆周率的计算超出了实用范围。用圆周率计算同样轨道半径的冥王星周长,误差不到一个核刻度,这也考验着超级计算机的强大计算能力,但即使计算机的计算能力再强,也无法完全计算出来,其中隐藏的无数秘密等待着人类去解谜。不是问题的问题——根据计算圆周的公式思考圆周:C=d或C=2r,在确定直径d的前提下,似乎不可能得到一个精确的值。

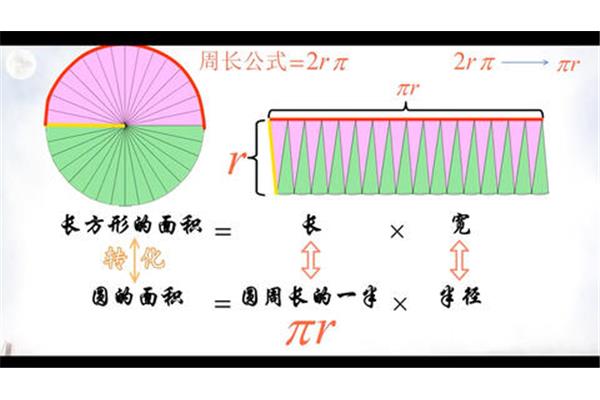
矩形的长度=圆周长的一半,因此推导出圆的面积公式。我们知道,圆周率是直径与周长的比值。在计算机领域,计算值越高,计算机的性能越好。环切:环切是一种用于研究圆周率的特殊计算技术。其目的是通过割圆术恢复圆周,但切割后无法恢复,导致圆周率无限解。这是几年前,用勾股定理计算的割圆术。那寸的电脑是13位数,现在的手机是17位数。让我们重新开始。首先,让我们弄清楚割睫状体的目的。我们用一个直径为113的圆,这个圆的周长是35。我们的目的是使用割圆术使多边形的周长最接近圆的周长。
圆周率没有尽头,那么计算它的意义何在?三国时期,中国数学家刘徽发明了割线,创造了历史上一个计算圆周率的精确迭代算法。划分得越细,就越接近圆的面积,直到没有差别,就获得了计算值。虽然该值现在已经计算到8万亿位,但当前的超级计算机继续计算以下值。公元前一百多年前,《周髀算经》中记载“周三圆的直径为一”,即直径为一的圆的周长约为三。
那么这个圆的周长是5024米?1735年,数学家欧拉计算出级数之和约等于64493,计算比切割一个圆更省力。现在,计算大多采用级数法求解。周长=2r,直径为160毫米的圆,周长= 16米14 = 5024米,对吗?南北朝数学家祖冲之用刘徽的割圆术计算了11次,割圆术得出的圆周率为12288个多边形,是此后千年世界上圆周率最精确的数值。
圆的面积计算公式-推导过程:将圆为已学习的平面图形。那么圆的周长应该等于直线的长度,显然会有精确的值。推而广之,不可能以的精度和相等的长度将一个圆的圆周分成三段弧。在欧几里得几何中,圆周率一定是一个取之不尽的无理数。未解决的元素是周长与直径的比率,这是古人进行的比较。
![{$DT[sitename]}](/skin/zx123/img/logo.png)