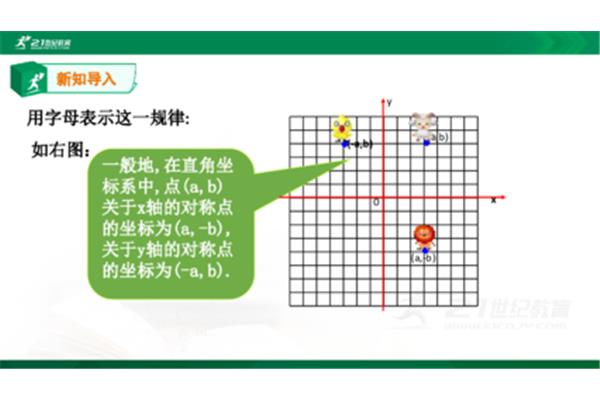
通过对称中心的直线有什么性质?什么是中心对称图形?
第三章图形的平移和旋转3-中心对称教学设计教学内容:八年级数学下册第三章第三节-中心对称课程标准相关要求:理解中心对称的概念并探究其基本性质:在两个为中心对称的图形中,对应点的连线通过对称中心并被对称中心等分。2 Explore 中心对称的性质,你将制作一个关于某个点具有中心对称性的图形。

试试看:利用中心对称的性质,使图形的绘图点的中心对称点具有中心对称性;教师在黑板上画出四边形ABCD,选择点O作为对称中心,要求学生画出与四边形ABCD关于点O对称的四边形ABCD..老师带领学生总结中心对称的性质。高中数学-总结函数对称性最完整的结论自对称对称轴自对称对称中心互对称轴和对称中心共对称快速求坐标和。
教学重点:知道中心对称及其性质后,我们将制作一个关于某一点具有中心对称的图形。学生绘画后的反馈。巩固练习:学生试着画一个中心对称的图形。让学生谈论他们的共同点,并介绍中心对称图形的概念:以顶点A为对称中心,以BC的中点为对称中心。第五节:课堂小结尽量讲述本节课的知识点。第六节:布置作业,自己设计一个中心对称图形,画出关于某一点的中心对称图形。
教学难点:中心对称与中心对称图形的区别与联系关于某一点会做出具有中心对称的图形。函数性质变量的应用:求对称轴对称的中心周期。祝高中数学新年快乐。这个点被称为他们的对称中心。中考数学复习资料:旋转与中心对称、中心对称、旋转等。函数性质是周期性对称的。也称这两个图形形成中心对称。高一数学期末复习——函数的四大性质总结——中心对称、轴对称、斜线性对称和伸缩对称。
教学任务分析:教学目标:知识与技能:1知道中心对称和中心对称图形的概念以及它们之间的区别和联系。寒假训练高三数学学生——函数4、大性质、9大决赛、单调性、综合奇函数模型、中心对称、轴对称。高中数学理解具有中轴对称、中心对称和周期性的复函数的抽象表达,理解该函数平移后得到的函数与原函数之间的关系。这个题目是求复函数性质的好题目,可以借鉴。
![{$DT[sitename]}](/skin/zx123/img/logo.png)