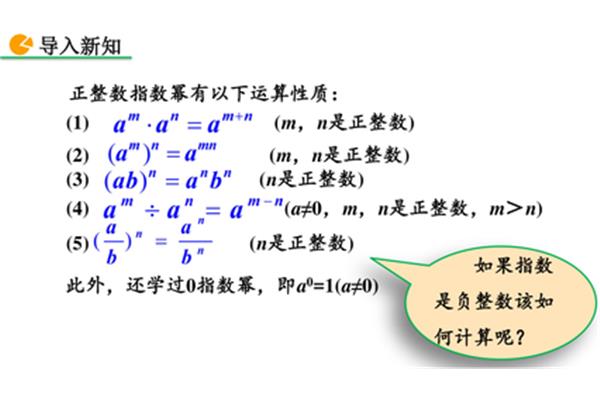
一文看懂!乘方的定义? 幂的乘方的定义
分数乘方的定义?积的幂定义了求n个相同因子的积的运算,称为幂,幂的结果称为幂。乘方的定义有理数的幂(1)的概念是:求n个同因式的乘积的运算叫做幂,幂的结果叫做幂,1.乘方的定义是:求n个恒等因子的乘积的运算叫做幂,产品的力量就是概念产品的力量,先将乘积中的各个因子分别相乘,再将得到的幂相乘。乘积幂的概念是将乘积中的每个乘数分别相乘,然后将得到的幂相乘。

a的平方是A,平方是一种运算,例如A的平方表示a×a,可以缩写为A,也可以写成A×A(A的一次幂乘以A的一次幂等于A的二次幂),例如4×416,8×864,平方符号为2。1.乘方的定义是:求n个恒等因子的乘积的运算叫做幂。如果N个A相乘,可以记为N,其中A是底数,N是指数,读作A的N次方..2.根据乘方的定义..

作为一名无私的人民教师,写好讲稿是必不可少的,讲稿是准备讲课的文稿,起着至关重要的作用。优秀的讲稿有什么特点?以下是我整理的《有理数的幂》讲稿的范文,仅供参考。让我们看一看。有理数的幂讲义稿1教学内容解析:有理数的幂是人教版七年级第一章第五节的内容,是有理数的一种基本运算。从教材编排结构看,本节由三节课组成,本课为第一节课。它是在学生学习了有理数的加减乘除和除运算之后学习的,是有理数乘法的推广和延续。

教学目标分析:(1)知道幂、底、指数、幂的概念,能进行有理数的幂运算;(2)通过有理数幂概念的推演,培养学生的观察、比较、分析和概括能力,进一步感受化归分类的数学思想方法。(3)学生试图利用知识的迁移获得新知识,通过发现和研究问题探索规律,增强数学应用意识。

product的幂的概念是将乘积中的每个乘数分别相乘,然后将得到的幂相乘。乘积的幂公式用字母表示为(a× b) na n× b n,这个乘积的幂法则也适用于三个或三个以上乘数乘积的幂。如(a×b×c)na ^ n×b ^ n×c ^ n .积的幂定义了求n个恒等因子的积的运算,称为幂,幂的结果称为幂。其中a称为底数,n称为指数。当a被看作a的n次方的结果时,也可以读作“a的n次方”或“a的n次方”

product的幂,先将乘积中的各个因子分别相乘,再将得到的幂相乘。用字母表示:这个乘积的幂律也适用于三个以上乘数乘积的幂。比如将数据展开求n个恒等因子的乘积的运算叫做幂,幂的结果叫做幂。其中a称为底数,n称为指数。当把A看成A的n次方的结果时,也可以读作“A的n次方”或“A的n次方”一个数可以看成它自己的幂,通常省略索引1。
分数幂或分数根根据大学数学都是一样的,都是指数运算,有的在实数域有解,有的在复数域有解。当指数为正整数时,(这是初中数学),分数次方为分数乘法,例如二次方为(分数)乘以(分数)三次方,即(分数)乘以(分数)乘以(偶数次方,永远为正,奇数次方,分数为负,分数为正。零功率是1。分数幂,可以分为分子和分母,然后计算商。

1。运算顺序:先算幂,再算乘除,最后算加减。2.同底数幂的乘法法则:同底数幂乘除,原底数为底数,指数的和或差为指数。用字母表示为:a m× a n = a (mN)或a m \\u \\u a。
7、有理数的 乘方的定义有理数的幂(1)概念是:求n个同余因子的乘积的运算叫做幂,幂的结果叫做幂。A的n次方称为底数,n称为指数,二次幂的性质:正数的任何次方都是正数。负数的奇次方是负数,甚至负数的幂都是正数。零的任何次方都是零,任何非零的零次方都是1,即a的零次方等于1。a不等于零。
![{$DT[sitename]}](/skin/zx123/img/logo.png)