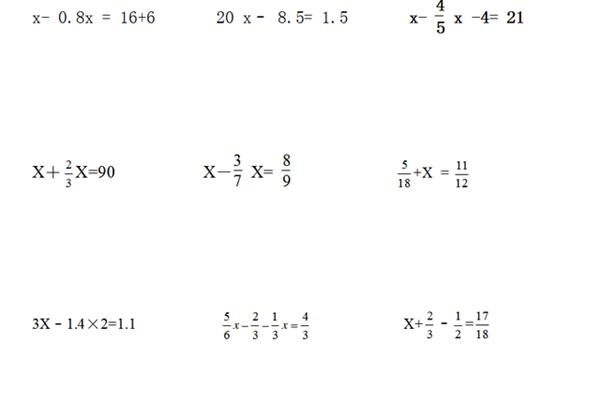圆的普通方程 x 2什么是圆的普通方程？圆的标准方程是什么？t是圆的圆心角，(0 ≤5t)求圆的方程的四种方法如下:1。直接法:从给定动点满足的几何条件出发列出方程，然后进行坐标代入和简化，得到所需的轨迹方程，这种方法称为直接法，如何推导圆的标准方程。

以原点为圆心，半径为r: xyr的圆；以(a，b)为圆心，半径为r: (xa) (Yb) r的圆；园的一般方程:X Y CX Dym0特点:①二次项的系数相等；②没有交叉项；1.圆的标准方程(X-A) (Y-B) r有三个参数A，B，R，只要找到A，B，R，此时就确定了圆的方程。所以确定圆的方程需要三个独立的条件，其中圆心坐标是圆的定位条件，半径是圆的成形条件。

process x 2y 22x4y40。(x1) x1)^2 (y 2)^210的意思是(x1) 2 (y 2) 21。圆心为(1，2)，半径为1。(x1)^2(2)^25。x ^ 2y 22x4y 40 >(x1)2(y ^ 2)21若圆心为(1，2)，半径为1，则参数方程为x1 cosα，y2 sinα。注:圆心为(x0，y0)，半径为r的圆的参数方程通常写成xx0 r*cosα，yy0 r*sinα。

设圆心为M(a，b)，半径为r，点P(x，y)为圆上任意一点，MP的长度为r，那么我们可以用两点间的距离公式。圆的一般方程为X Y DXEY F0 (DE4F > 0)，其中圆心坐标为(D/2，E/2)，半径公式为:推导过程:展开数据:1。在圆(XA) (Yb) R的标准方程中，有三个参数A，B，R，即圆心坐标为(A，B)，只要找到。

/图像-4//图像-5/1。(xa) 2 (Yb) 2r 2 (a，b)是中心坐标，r是半径2。x 2y 2 cxdye 03 . xr * cos(t)yr * sin(t)r为半径，t为圆心角，和。

例2:设圆心为m1，圆心为m2，运动圆与这两个圆外切，求运动圆的圆心p的轨迹方程。解法:设运动圆的半径为r，由两圆外切的条件得到。三、待定系数法:由题意可知曲线类型，将方程设定为曲线方程的一般形式，利用题中给定的条件即可得到所需的待定系数，进而得到轨迹方程。这种方法叫做待定系数法。4.参数法:选择合适的参数，分别用参数表示动点的坐标，得到动点轨迹的参数方程，然后消去参数，从而得到动点轨迹的一般方程。这种方法称为参数法。

在圆的标准方程(XA) (Yb) r中，有三个参数A，B，R，即圆心坐标为(A，B)。只要找到A，B，R，圆的方程就确定了。所以确定圆方程需要三个独立的条件，其中圆心坐标是圆的定位条件，半径是圆的成形条件。圆的一般方程:x y dxeyf0 (de4f > 0)。圆的端点公式:若两点A(a1，b1)和B(a2，

是圆的一般方程:x ^ 2y ^ 2 dxey F0(d ^ 2e 24f > 0)(x ^ d/2)2(y ^ e/2)2(d ^ 2e 24f)/4圆的半径是√[(d ^ 2e 24f)]。