0是有理数吗?0是正有理数吗？0是非理性的还是理性的？0是理性的。有理数包含0吗？0是有理数，不是无理数，0是实数吗？为什么0是实数？实数是有理数和无理数的统称，0是有理数，有理数是正整数、0、负整数和分数的总称，有理数集中的数可分为正有理数、负有理数和零。有理数包括0吗。

0是一个实数。0是介于1和1之间的整数。是最小的自然数，也是有理数。0既不是正数，也不是负数，而是正数和负数的分界点。实数是有理数和无理数的统称。数学上，实数定义为数轴上实数和点对应的数。实数可以直观地看作是有限小数和无限小数、实数和数轴上的点一一对应。在计算机领域，由于计算机只能存储有限的小数位数，所以实数往往用浮点数来表示。

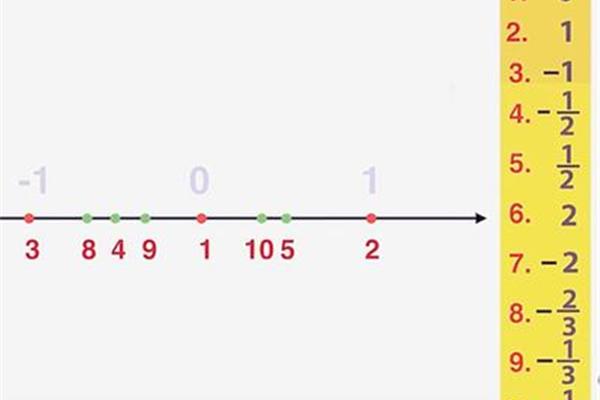
实数集通常用黑色字母R表示，R代表n维实数空间。实数是不可数的。实数是实数理论的核心研究对象。所有实数的集合可以称为实数系或实数连续统。任何完整的阿基米德有序域都可以称为实数系。在保序同构的意义上是唯一的，常以R表示，由于R是定义算术运算的算术系统，所以有实数系之称。

zero是有理数。对有理数的理解:1。有理数是整数(正整数，0，负整数)和分数的统称。正整数和正分数统称为正有理数，负整数和负分数统称为负有理数。因此，有理数集合的个数可分为正有理数、负有理数和零。由于任何整数或分数都可以转化为循环小数，反之亦然，所以每一个循环小数也可以转化为整数或分数，因此，有理数也可以定义为循环小数。2.有理数集是整数集的扩展。

3.关于有理数顺序的规定:如果是正有理数，当大于或小于时，记为或。任何两个不相等的有理数都可以比较大小。4.有理数集和整数集的一个重要区别是有理数集是稠密的，而整数集是稠密的。按大小顺序排列有理数后，任意两个有理数之间一定还有其他有理数，这就是密度。整数集没有这个特性，所以两个相邻整数之间没有其他整数。5.有理数是实数的紧致子集:每个实数都有任意一个闭有理数。

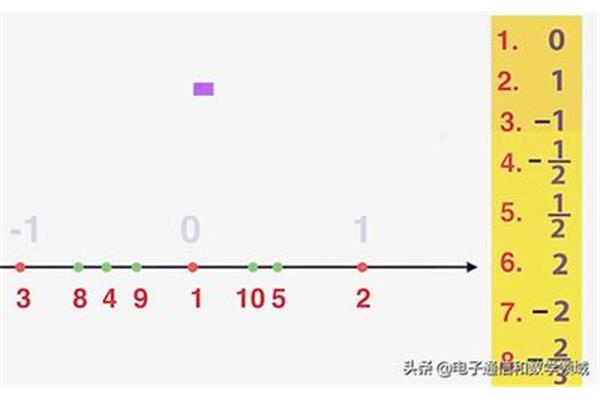
0是实数，是有理数和无理数的统称，而0是有理数，是正整数、0、负整数和分数的统称。有理数集中的数可分为正有理数、负有理数和零。有理数是:整数包括0，正负整数，有限小数如0.5，无限循环小数如1/3。无理数是圆周率、根号2等无限循环小数。0是介于1和1之间的整数。是最小的自然数，也是有理数。0既不是正数，也不是负数，而是正数和负数的分界点。

0是有理数，不是无理数。无理数也叫无限无环小数，不能写成两个整数之比。如果用十进制形式写，小数点后有无限多位，不会循环，所以0是有理数。常见的无理数有不完全平方数的平方根、π和E，无理数的另一个特点是无穷连分数表达。无理数是由毕达哥拉斯的一个弟子首先发现的。

当然。Rationalnumber:可以精确表示为两个整数之比的数。包括整数和分数，也可以表示为有限小数或无限循环小数。这个定义适用于十进制和其他十进制(如二进制)的数字。比如3，98.11，5，7/22都是有理数。有理数是指一个非无限的无循环小数，所以0也是有理数。0属于有理数，有理数是分数，整数，无理数是无限无环小数，比如吴。

0是一个有理数。无理数是无限循环的小数，所以零是有理数。有理数是正整数、0、负整数、分数的统称，所以0是有理数。有理数是数学科学中的一个数的概念和定义。有理数是由整数和分数组成的集合的总称。正整数、负整数、0、分数都是有理数。0是有理数，不是无理数。0是介于1和1之间的整数。0是最小的自然数，0既不是正数也不是负数，0是正数和负数的分界点。

No .概念:正有理数是指数学术语。除了负数、零和无理数之外，正有理数可以精确地表示为两个整数之比。有理数:有理数是指可以看作分母为1的分数的整数。正整数、0、负整数、正分数、负分数都可以写成分数的形式，这样的数叫做有理数。有理数的小数部分是有限的或循环的。不是有理数的实数叫做无理数。无理数:无理数，即无理数的实数，不能写成两个整数之比。

是有理数是整数(正整数，0，负整数)和分数的统称，所以0是有理数。0是一个极其重要的数字，0的概念在其他地区已经存在很久了。公元前3000年，巴比伦人知道如何用零来避免混乱。在古埃及，早在公元前2000年，就有人在记账时用特殊符号记录零。玛雅文明首先发明了特殊字体0。在玛雅数字中，0由一个像贝壳一样的象形符号表示。标准数字0是在公元5世纪左右由古印度人发明的。

在东方的GJ，数学主要以运算为主(在西方，印度人的9个数字一开始是用几何书写的，所有数字都可以用阿拉伯人发明的0符号书写)。因为某些原因，0这个符号刚传入西方的时候，一度在西方引起混乱，因为当时西方认为所有的数字都是正数，数字0会让很多公式和逻辑站不住脚(比如除以0)，甚至认为它是魔鬼数，所以禁止使用，直到大约15、16世纪，零和负数才逐渐被西方人所认识，从而导致了西方数学的迅速发展。