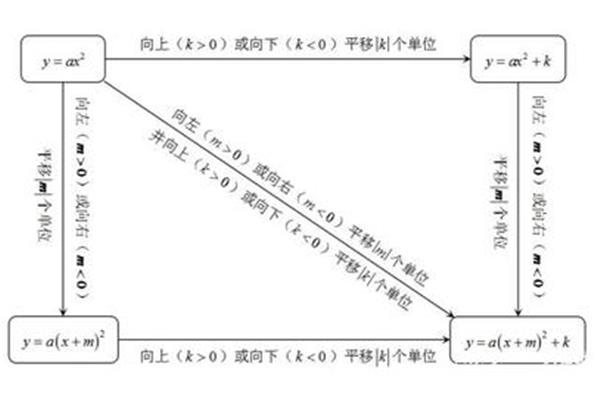
二次函数的特点解决了二次函数的内涵和本质。二次函数Yax2 BX C (A ≠ 0，A，B，C为常数)包含X和y两个变量，只要我们先确定其中一个变量，就可以用解析式求出另一个变量，即可以得到一组解，而一组解就是一个点的坐标，其实二次函数的图像就是无数个这样的点组成的图形，2.熟悉几个特殊二次函数的图像和性质，1.通过描点观察yax2、Yax2 K、Ya (x H) 2图像的形状和位置，熟悉各图像的基本特征。相反，你可以根据抛物线的特点，很快确定它是哪一个解析式，左加右减”，yax2 → ya (x h) 2 k“加减”是针对k的，“左加右减”是针对h的，简而言之，如果两个二次函数的二次系数相同，则它们的抛物线形状相同，但由于顶点坐标不同，位置不同，抛物线的平移本质上就是顶点的平移，如果抛物线是一般形式，理解并明确解析式的特征与图像的特征是完全对应的，解题时，我们的脑海中要有一个画面，看到函数，就能在脑海中反映出它的形象的基本特征。4、。

求解二次函数的内涵和本质。二次函数Yax2 BX C (A ≠ 0，A，B，C为常数)包含X和y两个变量，只要我们先确定其中一个变量，就可以用解析式求出另一个变量，即可以得到一组解。而一组解就是一个点的坐标，其实二次函数的图像就是无数个这样的点组成的图形。2.熟悉几个特殊二次函数的图像和性质。1.通过描点观察yax2、Yax2 K、Ya (x H) 2图像的形状和位置，熟悉各图像的基本特征。相反，你可以根据抛物线的特点，很快确定它是哪一个解析式。左加右减”，yax2 → ya (x h) 2 k“加减”是针对k的，“左加右减”是针对h的，简而言之，如果两个二次函数的二次系数相同，则它们的抛物线形状相同，但由于顶点坐标不同，位置不同，抛物线的平移本质上就是顶点的平移。如果抛物线是一般形式，理解并明确解析式的特征与图像的特征是完全对应的。解题时，我们的脑海中要有一个画面，看到函数，就能在脑海中反映出它的形象的基本特征。4、。

当ya (xh) Ka0时，xh增加。Ya (XM) 2 k (a/0) a > 0，在(m，无穷大)上单调递增，在(无穷大，m) a上单调递减。