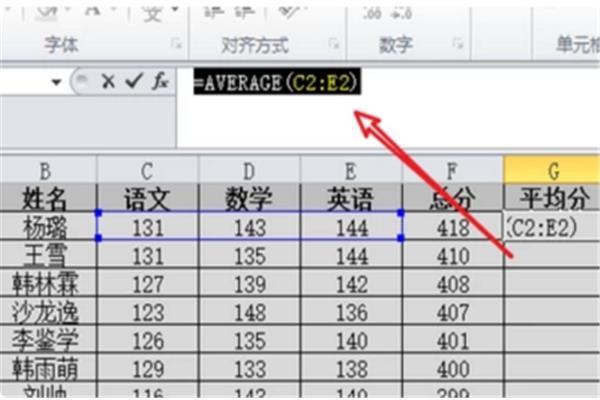
加权平均数的意义 算术平均数的意义
均值和众数均值:它反映的是一组数据的平均大小,均值众数实际上就是均值:它反映的是一组数据的平均大小,均值的概念和对均值的解释(1)从统计学的角度来看,均值是定量评价每个数据点的普遍性,确定平均水平,而中位数是从中等数据点开始把数据分成两半的度量。平均值和中位数的计算方法和意义不同,所以有不同的参考值,首先,平均数更具有代表性和普遍性,平均值是基于所有数据的,所以能充分反映数据的整体情况,当数据量足够,被调查人群相对均匀时,平均值具有更可靠的参考价值。

其次,中位数更具有典型性和实用性。中位数是将各种数据按大小顺序排列后,位于中间位置的一个数值。更能反映被访人群的中间水平和实际情况,更具典型性和实用性。当数据分布不均匀或存在极值时,中位数的参考值可能会超过平均值。比如对于一些高收入或低收入群体,中位数更能反映群体的平均水平。所以对于这个数据,“一季度全国平均月薪10101元”,无论是平均值还是中位数都有参考价值。
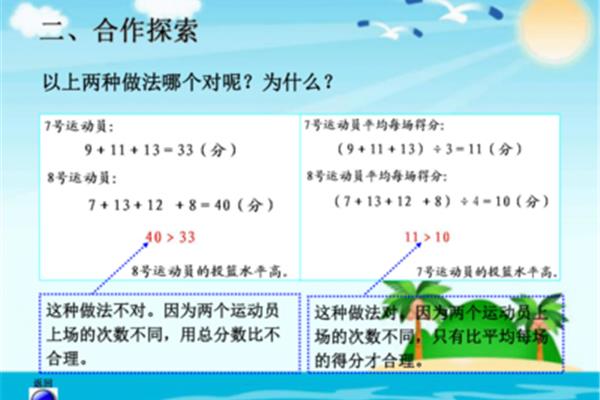
第二期的平均数教学要通过刻画,引导学生了解熟悉情境中平均数的代表性。第二期的目标是认识自然数,小数和分数形成后,我们就开门见山,初步认识小数和分数;能够进行复杂的整数四则运算和小数、分数的简单加减运算,理解运算规律。愿意了解日常生活中与数学相关的信息,愿意参加数学学习活动。形成数感、运算能力和初步的推理意识。懂平均数的意义,用平均数解题;

在主题活动中,要进一步了解时间单位和方向,了解质量单位,尝试运用数学等学科的知识和方法解决问题,积累数学活动的经验。平均数的概念:平均数,一个统计学术语,是代表一组数据中趋势的量,指的是一组数据中所有数据的总和除以该组数据的个数。它是反映数据集中趋势的指标。用于表示平行数据中观测值相对集中的中心位置。解决平均应用问题的关键是确定“总量”和总量对应的总份数。

理论我就不说了。简单来说:在一组数据中出现频率最高的数据称为这组数据的众数中位数。n个数据按大小顺序排列,中间位置(或)的数据称为这组数据的中位数平均值,不用说了吧?和小学的意思一样。众数:一组数中出现频率最高的数,可以是两个或两个以上,也可以没有中位数:一组数按大小排列,中间的数,如果有两个,就是它们的平均数。

1。平均值:一组数据。用这组数据的总和除以总分,得到的数就是这组数据的平均值。平均数的大小与一组数据中的每一个数据有关,任何一个数据的变化都会引起平均数的变化,即平均数受到一个较大数字和一个较小数字的影响。2.中位数:将一组数据按大小顺序排列,称中间位置的一个数(或中间位置的两个数的平均值)为这组数据的中位数。中位数的大小只与数据的排列位置有关。
3.模式:在一组数据中出现频率最高的数据称为该组数据的模式。因此,寻找一组数据的模式不需要计算或排序,只需要统计出现次数较多的数据的频率即可。众数和概率有密切的关系。模式的大小只与一组数据中的某些数据有关。当一组数据被多次重复时,其模式往往是我们所关心的集中趋势。
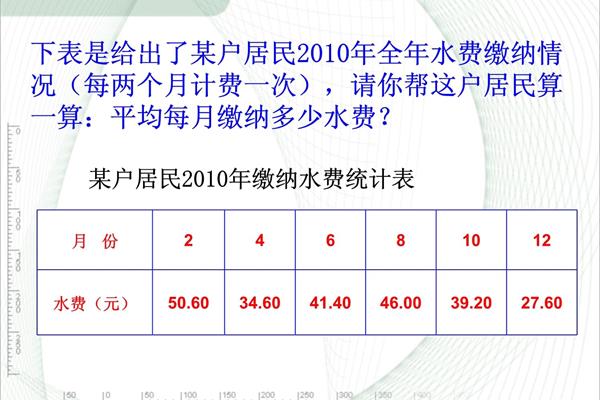
average可以反映一组数据的平均水平,众数是在一组数据中出现最频繁的数,即众数可以反映一组数据的多数水平,中位数是一组数据中间的数(当有奇数个数据时)或中间两个数的平均值(当有偶数个数据时),所以中位数可以反映一组数据的中间水平。描述分数、权重标准等时使用平均值。,描述一组数据的中间水平和集中趋势时的中位数,描述一组数据的多数水平时的众数。

1.定义不同的平均数:一组数据的总和除以这组数据的个数得到的商称为这组数据的平均数。中位数:将一组数据按大小顺序排列,中间位置的一个数称为这组数据的中位数。众数:在一组数据中出现频率最高的数字称为这组数据的众数。2.求解不同平均数:将所有数据之和除以数据个数,需要计算得出。

average:反映一组数据的平均大小,常用来表示数据的整体“平均水平”。中位数:像分割线一样,把数据分为前半部分和后半部分,所以用来表示一组数据的“平均水平”。众数:反映出现次数最多的数据,用来表示一组数据的“多数水平”。虽然这三个统计数字反映了不同的情况,

这里的极值指的是过大或过小的数。数量太大时会提高平均值,数量太少时会降低平均值。中位数:与数据的排列位置有关,有些数据变化对其没有影响;它是一组数据中间位置的代表值,不受数据极值的影响。模式:与数据出现的频率有关,重点考察每一个数据出现的频率,其大小只与这组数据中的部分数据有关,不受极值的影响。
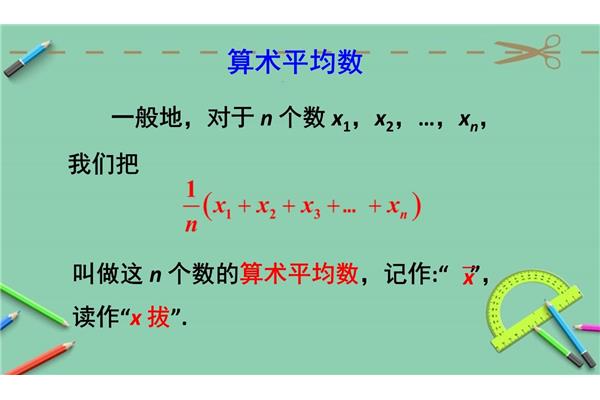
算术平均又称均值,是统计学中最基本、最常用的平均指标,可分为简单算术平均和加权算术平均。算术平均在统计学中占有重要的地位,是统计分析和推断的基础。它的数学性质有以下含义:1。第一,从统计学的角度来看,它是一组数据的重心,是数据误差相互抵消的必然结果;2.其次,算术平均值有一些重要的数学性质,如:变量值与其算术平均值的偏差之和等于零,变量值与其算术平均值的偏差平方和最小。

average是一组数据大小均匀分布后得到的数值,该组中的其他数据围绕这个平均值上下波动。总数÷平均份数。平均值是一个“虚”数,是一组数据之和除以该组数据的个数(即先组合一组被除的数,再平均除)得到的商。是借助平均分的意义计算出来的,而不是这组的实际数据。

average:反映一组数据的平均大小,常用来表示数据的整体“平均水平”。众数:反映出现次数最多的数据,用来表示一组数据的“多数水平”。平均数与每一个数据都有关系,任何数据的变化都会引起平均数相应的变化。主要缺点是,当它显得太大时,它很容易受到极值的影响,其中极值是指太大或太小。
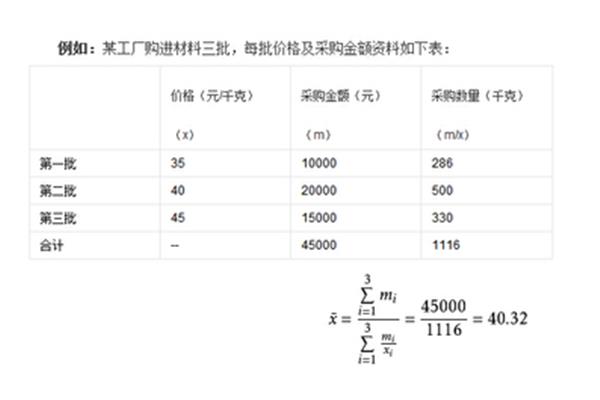
9、平均数的概念及意义平均数的解释(1)【平均数】(2)几个数之和除以这些数的个数得到的商。例如,(5 6 7)÷36,6是5,6,7的平均值,(3)取一笔钱或一个量若干年的平均降雨量,详细说明两个或两个以上数之和除以相加数所得的商。如果(3 5 7) ÷ 3 = 5,5就是3、5、7的平均值,分解层次这个词的解释是平的,没有倾斜和不平,像一个静止的水面:平地。
![{$DT[sitename]}](/skin/zx123/img/logo.png)