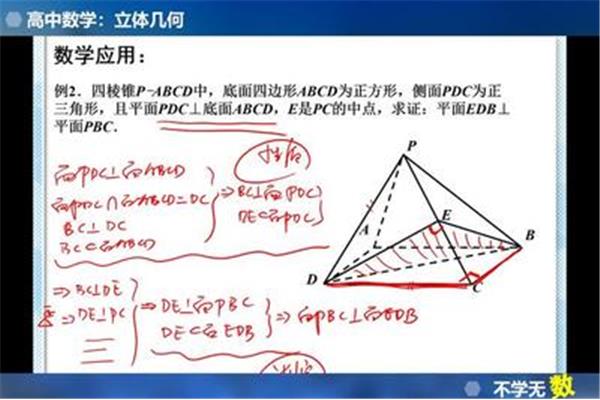
如何证明线面垂直?一般可通过证明一面的直线/斜线/-1
高一下立体几何,今天讲解线面垂直和面面垂直的性质定理,和判定定理,性质定理比较简单,我觉得只需要给学生说明白,面的本质在这里是两条相交直线即可,证明线面垂直就是证明线与两条相交直线垂直即可。面面垂直本质是线面垂直,然后这条线在面内即可,当然性质定理很重要,性质定理高考属于必考范围,高一时候讲的明明白白,高三都给忘。
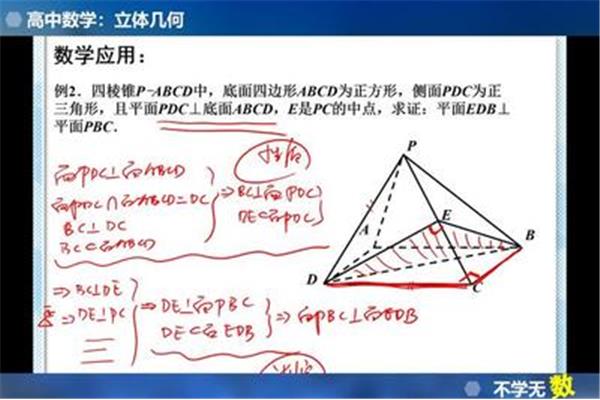
可以通过证明一面的直线/另一面的-1。换句话说,如果直线l 垂直在平面α上,那么包含直线L的所有平面都是垂直在α上。以两个面的交线上的任意一点为垂足,用交线垂直引出一条直线到每个面。如果两条线是直的垂直,那么两个面也是垂直。证明一个面上的一条线垂直另一个面。证明 Face 垂直的基本方法如下:(1)利用证明的定义,即利用两个平面的交点形成一个直的二面角证明;(2)利用平面垂直 证明的判定定理,即如果a⊥,一个⊥在证明两个平面垂直中,一般方法如下作为辅助线,应该有理论依据,对证明有利,不能随意添加。当有平面垂直时,一般需要利用性质定理作平面内交线的垂线。做成线面 垂直。解决这类问题的关键是掌握“line垂直”“surface线面”。

face 垂直:两个平面互为垂直。如果一个平面上的直线在它们的交点处是垂直,那么这条直线在另一个平面上就是垂直。直二面角的性质:若两平面互为垂直,则它的直二面角的一边在另一平面上为垂直。如果两个平面相互垂直,那么在一个平面内垂直它们相交的线垂直在另一个平面内。已知:α ⊥ β,α∪βl,O∈l,OP⊥l,OP⊂α.证据:OP⊥β.
∵ α ⊥ β ∴∠ POQ 90,即OP ∵ OQ ≁ L,l∩OQO,L β,OQβ ∴ OP ⊥ β扩展数据:性质定理:性质。性质定理2:只有一条直线垂直已知平面通过空间中的一点,定理3:如果两条平行线中的一条在一个平面上是垂直,那么另一条在这个平面上是垂直。
![{$DT[sitename]}](/skin/zx123/img/logo.png)