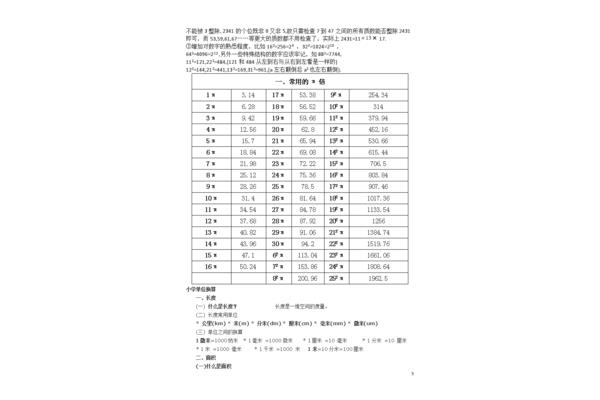
异分母分数的大小比较 四年级分数的大小比较
如何比较分数的大小?同样大小的分子相同,但分母大的分数更小。六年级比较年级大小的一个简单方法比较年级大小的几种方法我们遇到比较年级大小的问题,往往用分数和小数共用的方法来解决,分数比公式:对于分子相同的两个分数,分母小的分数较大,分母大的分数较小;分母相同的两个分数,分子大的分数大,分子小的分数小。

分数比公式:对于分子相同的两个分数,分母小的分数较大,分母大的分数较小;分母相同的两个分数,分子大的分数大,分子小的分数小。1分数的定义,一个分数代表整体的一部分,或者更一般地说,代表任意一个数量相等的部分,一个分数描述的是一定大小的一部分,比如二分之一,八分之五,四分之三。分子和分母也用于不常见的分数,包括复合分数,复杂分数和混合数。
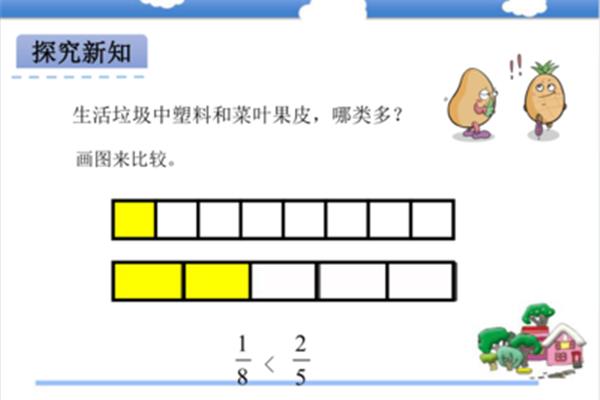
将单位“1”平均分成几个部分,代表这样一个或几个部分的数字称为分数。分子在上,分母在下。2.把一个物体或图形平均分成几个部分,取其中的几个,就是这个物体或图形的分数。一个整体被平分的份额越多,每一份所代表的数字就越小。3.分母相同的分数相加:分母不变,分子相加。分母相同的分数减法:分母不变,分子减法。分数减去1:1可视为分子分母相同的分数。
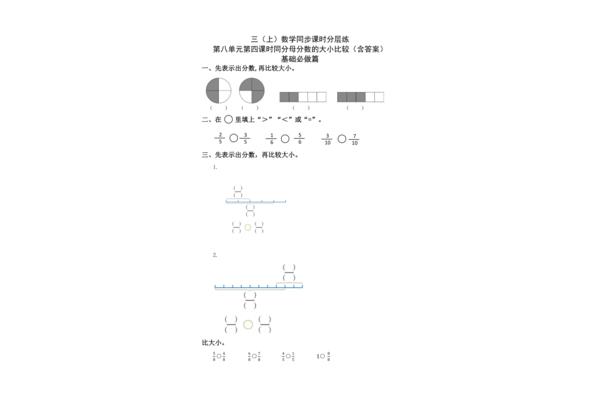
比较分数大小的几种方法我们会遇到比较分数大小的问题,这种问题往往通过分享和十进制的方法来解决。了解以下方法可能会帮助你更好地解决问题。1.用分子比较3/14和5/22的大小如果用分母的话,计算起来会很复杂,分子法要省力很多。3/1415/70,5/2215/6615/70 < 15/66,即3/14 < 5/22,是比较分母大、分子相对小的分数最合适的方法。

据观察,这两个分数的分子和分母大小相同。从1中减去19/21和21/23,通过比较两个差值来比较原始分数。19/2112/2121/2312/23÷2/21 > 2/23∴12/21 < 12/23,即19/21 < 21/233,叉乘是将分子和分母交叉相乘得到的乘积进行比较。包含在较大产品中的分子具有较大的份额。

如果分母和分子不一样,可以先除以,使分母一样,再比较。比如3/4和4/5对比3/412/204/516/20的尺寸,那么3/4可以上什么档次?跟你打个比方吧。例1:二分之一和三分之一(不用看就知道分子的二分之一是一样的,分母小,但是分子是一样的,但是分母小)。例2:二分之一和三分之二(这意味着两个分数都是3分,4∴二分之一<三分之二)。
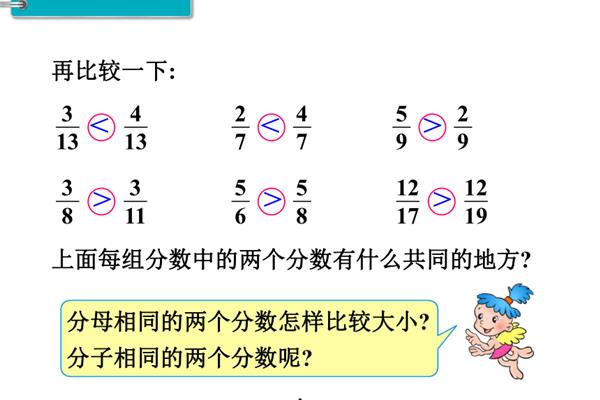
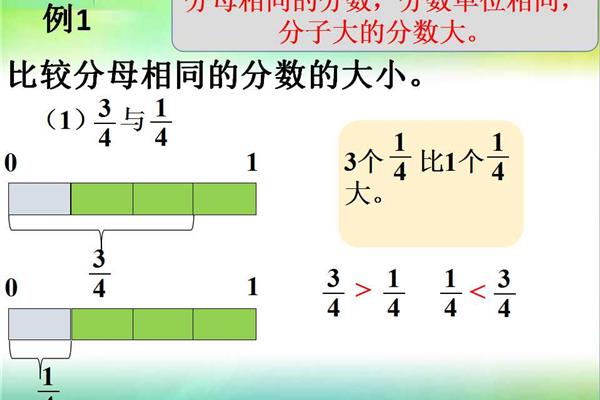
分子相同,但分母较大的分数较小。分母一样,分子越大分数越大。分子相同,分母越小,分数越大。分子和分母同时被同一个数(0除外)相乘或相除,分数的大小不变,这是分数的基本性质。分子在上面,分母在下面。也可以看作是除法,分子除以分母(因为0在除法中不能被除,所以分母不能是0)。相反,除法也可以用分数来表示。扩展数据:分母一定不能是0,因为分母相当于除数。
如果分母相同,分子越大,分数越大。如果是同一个分子,分母越大,分数越小。如果是分母不同,就要分。如果比较两个(或更多)分数,同时将两个(或更多)数的分母乘以分母的公倍数。分子越大,分数越大。比较两个分数时,1。分母相同,分子越大,数值越大;2.分子相同,分母越小,数值越大;3.当分母和分子不同时,就要把分数的分母或分子分成同一个,进行比较。
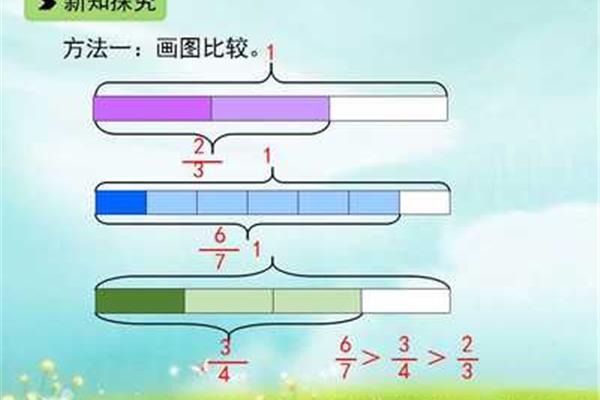
分数大小的比较分为两种:一种是分母相同,分子不同;第二,分子相同,分母不同。当比较两个分母相同、分子不同的分数时,在单位“1”相同的情况下,分数的分母相同,说明它们的分数单位相同。分子越大,它需要的拷贝就越多,也就是说,它包含的分数单元就越多。所以分母相同的分数比分子大的分数大。比如and,2/3表示2,1/3表示1/3,2大于1,所以>。
也就是说,比较两个分子相同分母不同的分数时,要看分数的分母。分母是平均份数更多,但每份更小,所以对于分子相同的两个分数,取相同的份数,分母较小的分数较大。如:>,写法:分数中间的横线叫分数线,分数线以上的数叫分子,分数线以下的数叫分母。把它当成分数来读,分数可以表示为除法公式:例如,一半等于1除以2。
![{$DT[sitename]}](/skin/zx123/img/logo.png)