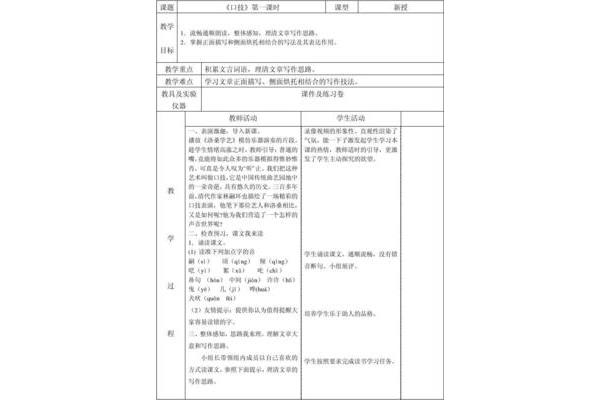
连续可积可导可微的关系如下
员工销售心得分享年初的一天下午5点左右来了一个常客,这次我看帅哥还带了个朋友,忙上前问侯,新年好!来来来先坐下下,喝杯茶的.他也答到这个好.每次来你都这么热情不买东西都不好意思。我说没关系的,喝茶随时都可以有的,招呼着他们先坐下喝茶..接着帅哥又说:今天特意带我朋友来你这里买东西的,我忙说好好谢谢谢谢支持,忙把倒好的茶递给他们。

边聊着天.跟据他朋友肖总的需求成功配了几份礼品,高兴的成交了500多元,也加上了肖总的微信并激活,成为我们的会员,.我说你以后需要都可微我哈可送货上门的,肖总说这么好还可送货上门,要的要的以后送礼就找你,果服务没的说了。我说这些都是我的工作,应该做的,你们满意就好,需要记得一定随时呼我哈其实我只是做了自已该做的,却得到顾客的满意.让我更加懂的把顾客当朋友,

连续可积可导可微的关系如下:可导与连续的关系:可导一定是连续的,连续不一定可导;可微与连续性的关系:可微与可微性相同;可积与连续的关系:可积不一定连续,连续一定可积;可微性与可积性的关系:可微性一般是可积的,可积性不能推导出某种可微性。对于多元函数,没有导数概念,只有偏导数存在。某处函数可微等价于所有方向的方向导数存在,只有偏导数存在不一定是可微,所以有:可微>偏导数存在>连续性>可积性。
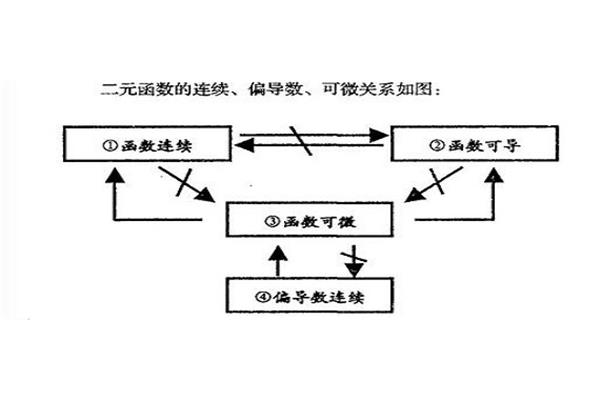
然后说y在xx -0的二阶/定义公式:δy/δxlim(δx > 0)(f(0 δx)f(0))/δxa。二元函数可微的定义是函数zf(x δ x,y δ y) f (x,y)在点(x,y)的全增量,可表示为δ za δ x b δ y o (ρ)。设xy0,则全增量为δZF(δx,δy)f(0,0),符号δx,δy换成x,y来表示。本题中(x,y) → (0,0)时函数f(x,y)的δZF(x,y) f (0,0) 2x y o (ρ)满足定义的要求,所以f(x,y)在点(0,0)/1233。
所以,如果P(x,y)以一种特殊的方式趋向P0(x0,y0),比如沿着一条固定的直线或曲线,即使f(x,y)无限接近某个值,我们也不能断定函数的极限是存在的。另一方面,如果当P(x,y)以不同的方式趋向P0(x0,y0)时,f(x,y)趋向不同的值,那么可以断定这个函数的极限不存在。
![{$DT[sitename]}](/skin/zx123/img/logo.png)