二分法是一种常用的算法，它可以用来解决复杂的数学问题，特别是求解多元函数的根。它的原理是，通过将一个数学问题分解成两个子问题，然后分别解决它们，从而达到解决整个问题的目的。

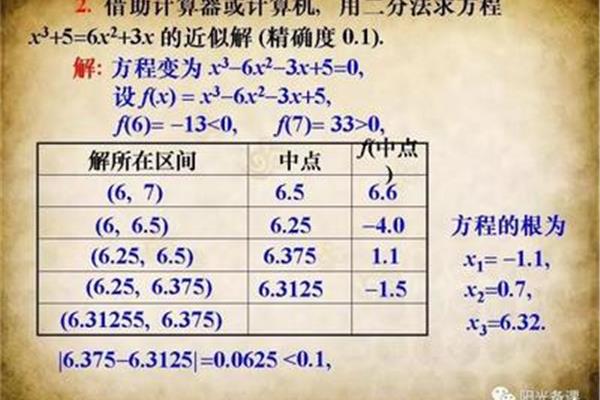
二分法的精确度取决于求解过程中的步骤数，即每次取中点时选择的区间宽度。一般来说，步骤数越多，精确度越高。由于二分法是一种分治算法，它的精确度受到取中点的宽度的限制，因此，当取中点的宽度越小时，精确度越高。

此外，二分法的精确度还受到求解过程中的误差的影响。当求解过程中的误差越小时，精确度越高。因此，在求解过程中，可以采用一些技巧来减少误差，从而提高二分法的精确度。例如，可以采用数值积分的方法求解函数，从而减少求解过程中的误差。

另外，在求解过程中，可以采用一些技巧来提高二分法的精确度。例如，可以采用多点二分法来求解函数，这样可以更有效地提高精确度。此外，可以采用改进的二分法，如牛顿迭代法等，以提高精确度。

总而言之，二分法的精确度受到取中点的宽度、求解过程中的误差以及采用的技巧的影响。因此，要提高二分法的精确度，需要通过减少取中点的宽度、减少求解过程中的误差以及采用改进的技巧等方法来实现。