直线是一种基本的几何图形，它是由两点确定的，也就是说，只要知道两点，就可以求出直线方程。

首先，我们需要知道两点的坐标，比如点A（x1，y1），点B（x2，y2），这两点就可以确定一条直线。两点确定一条直线的方法是：用两点的坐标求出直线的斜率k，再根据斜率k和其中一点的坐标（比如点A）求出直线方程的常数项，最后就可以得到直线方程了。

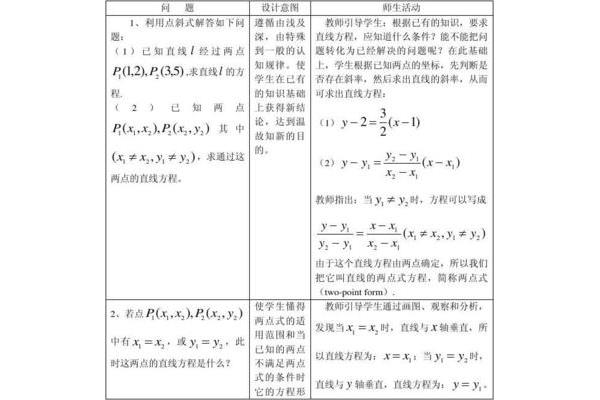
具体求法如下：

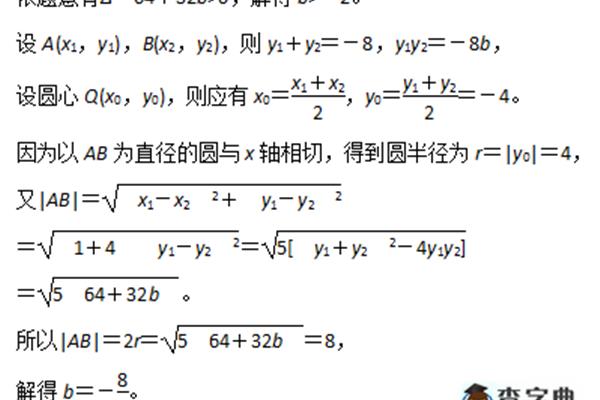
1. 求斜率：用两点的坐标求出斜率，斜率的计算公式为：k=（y2-y1）/（x2-x1）

2. 求常数项：用一点的坐标和斜率k求出常数项，计算公式为：b=y1-k*x1

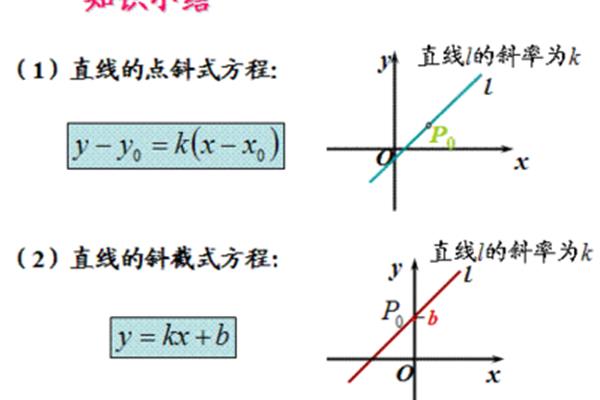
3. 组合求出直线方程：将斜率k和常数项b组合求出直线方程，直线方程的一般式为：y=kx b

以上就是两点求直线方程的方法，它非常简单，方便，只需要知道两点的坐标就可以求出直线方程。

两点求直线方程的方法广泛应用于几何学中，它可以帮助我们计算出两点之间的距离，求出圆的半径等等，同时也可以用来判断两点是否在同一条直线上。

总之，两点求直线方程是一种简单而有效的方法，它可以帮助我们解决许多几何问题，同时也可以作为绘制图形的基础。